Matemaattisia kaavoja ja merkintöjä voi kirjoittaa käyttäen Moodlen oletustekstieditoria Atto HTML:ää. Editorissa on käytössä kaavaeditori, josta saa nopeasti keskeisiä operaattoreita ja symboleita. Lisäksi tekstiä voi vapaasti muokata TeX- notaation avulla (ei LaTeX).
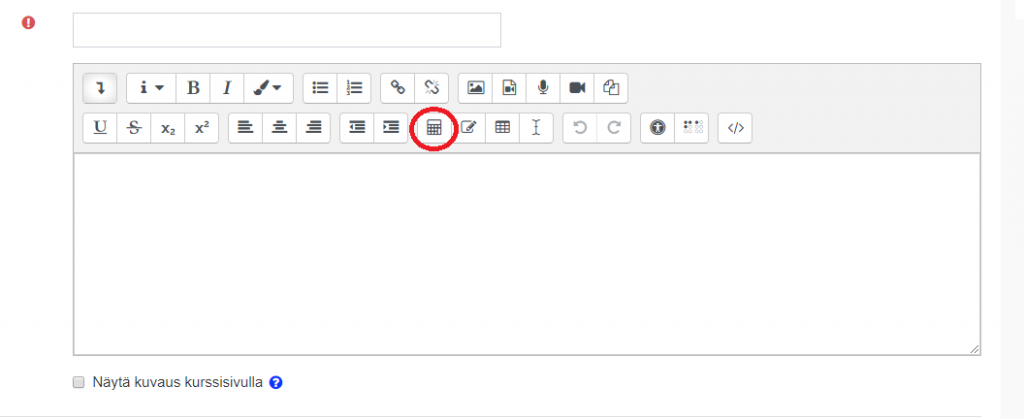
Kaavaeditorilla on valmiiksi asetettu keskeisimpiä operaattoreita, valikoima nuolia, kreikkalaiset aakkoset sekä valikoiman matemaattisia lausekkeita, joiden sisältöä voit muokata kaavaeditorin muokkausikkunassa. Esikatseluikkunassa näet lausekkeen kirjoitettuna. Kaavaeditorin merkinnät erotetaan varsinaisesta tekstistä \( -merkeillä, jota voit hyödyntää myös ilman editoria.
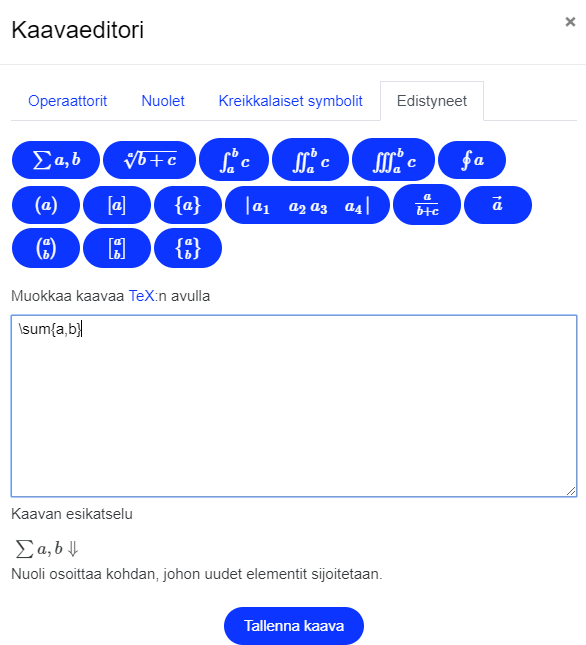
Tämän lisäksi voit kirjoittaa editoriin suoraan ilman kaavaeditorin käyttämistä mitä tahansa matemaattista tekstiä käyttäen TeX-notaatiota, jossa matemaattinen teksti erotetaan varsinaisesta tekstistä $$-merkeillä. Esimerkiksi $$ \vec{a} $$ näyttää vektorimerkintää käyttäen vektorin a.
Seuraavat kaavat on kirjoitettu tekstinä Moodlessa ja alla näet kuinka ne näkyvät oppimisympäristössä:
Murtoluvut: \( 1 \frac{2}{3} \), \( \frac{a}{b} + \frac{c}{b} = \frac{a+c}{b} \)
Potenssit: \( 2^3 \), saadaan tehtyä myös normaaleilla tekstinmuotoilutoiminnoilla, esimerkiksi x-2
Neliöjuuret: \( \sqrt{2}, \sqrt[3]{9} \)
Sulkujen käyttö: \( \left( 2 \times( 2+4) \right), \left( (2 \times 2)+4 \right) \)
Operaattoreita: \( \neq, \pm, \approx, \Delta, \nabla, A \cup B, \)
Vektorimerkintä: \(\vec{a}\) Lukujoukot: \( \mathbb{N} = {0, 1, 2, 3,…}\)
Funktiota: \( x^2 + y^2 = 1 \) \( f(x)=y \) \(f(x)=ax^2+bx+c\) \((2^m)^n = 2^{mn} \), kun \(m, n \in \mathbb{Z}\)
Hieman muokkaamalla kaavaa voit tehdä myös monirivisiä kaavoja ja funktioita.
\[f: \mathbb{R} \rightarrow \mathbb{R}\] \[f(x)=\lbrace {\frac{1}{x}}, kun \ x\neq 0\] \[f(x)=\lbrace{0}, kun \ x= 0\]
