Oppimistehtävä 1 – harjoitustehtävät
Ensimmäisen asteen yhtälöt
Yhtälö on kahden luvun tai lausekkeen merkitty yhtäsuuruus. Yhtälön ratkaisu on sen juuri.
Yhtälönratkaisu 1
Tee sama laskutoimitus yhtälön molemmille puolille.
Esim. 1
Ratkaise ![]() .
.
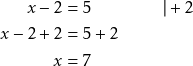
Ratkaise ![]() .
.
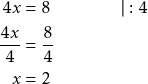
Yhtälönratkaisu 2
Jos vaihdat termin puolta, muuta sen etumerkki.
Esim. 2
Ratkaise ![]() .
.
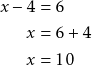
Yhtälönratkaisu 3
Yhdistä samankaltaiset termit siirtämällä ne samalle puolelle.
Esim. 3
Ratkaise ![]() .
.
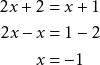
Kirjoitetaan yleinen ohje yhtälön ratkaisuun.

Lausekkeen käsittely
Kirjoitetaan kertolaskun määritelmän mukainen laskutoimitus.
![]()
Kirjoitetaan osittelulait.
![]()
Kun lauseke kerrotaan luvulla, kerrotaan lausekkeen jokainen termi kyseisellä luvulla. Lopuksi yhdistetään samanmuotoiset termit.
Esim. 4
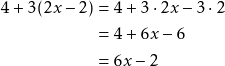
Tulon etumerkki riippuu sen tekijöistä.
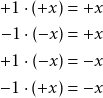
Esim. 5
![]()
Kirjoitetaan laskujärjestys.
![Rendered by QuickLaTeX.com \[ \left\{ \begin{array}{lccc} \text{aina ensin} ~ &( & & ) \\ \text{vasta sitten} ~ & \cdot & / & : \\ \text{viimeiseksi} ~ & + & / & - \\ \end{array} \right. \]](https://blogit.gradia.fi/matvalinnainen/wp-content/ql-cache/quicklatex.com-6de69b21a264039930555d5bba4b2997_l3.png)
Yhtälönratkaisu 4
Poista sulkumerkit suorittamalla tutut laskutoimitukset.
Esim. 6
Ratkaise ![]() .
.
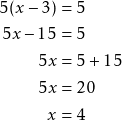
Yhtälönratkaisu 5
Poista nimittäjät kertomalla yhtälö sopivalla luvulla.
Esim. 7
Ratkaise ![]() .
.
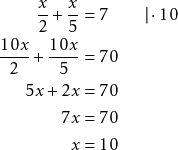
Jako-ongelmia
Matemaattisessa ongelmanratkaisussa (1) merkitse tuntematonta ![]() :llä, (2) lausu muut suureet tuntemattoman avulla, (3) kirjoita yhtälö, (4) ratkaise yhtälö ja (5) tarkasta tulos.
:llä, (2) lausu muut suureet tuntemattoman avulla, (3) kirjoita yhtälö, (4) ratkaise yhtälö ja (5) tarkasta tulos.
Esim. 8
Jaa 480 € A:n, B:n ja C:n kesken siten, että B saa kaksi kertaa niin paljon kuin A ja C saa 30 € enemmän kuin B.
Ratkaisu
(1) Merkitään tuntematonta ![]() :llä ja (2) lausutaan muut suureet tuntemattoman avulla.
:llä ja (2) lausutaan muut suureet tuntemattoman avulla.
A saa summan ![]() .
.
B saa summan ![]() .
.
C saa summan ![]() .
.
(3) Kirjoitetaan yhtälö ja (4) ratkaistaan se.
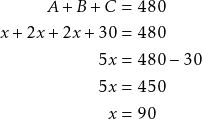
(5) Tarkastetaan tulos.
![]()
Vastaus
A saa 90 €, B saa 180 € ja C saa 210 €.
Esim. 9
Kalasaaliista kolme neljäsosaa tulee verkolla, viidesosa katiskalla ja kolme kalaa ongella. Laske kalojen lukumäärä.
Ratkaisu
(1) Merkitään tuntematonta ![]() :llä ja (2) lausutaan muut suureet tuntemattoman avulla.
:llä ja (2) lausutaan muut suureet tuntemattoman avulla.
Koko kalasaalis on ![]() .
.
Verkolla saadaan saalis ![]() .
.
Katiskalla saadaan saalis ![]() .
.
Ongella saadaan ![]() kalaa.
kalaa.
(3) Kirjoitetaan yhtälö ja (4) ratkaistaan se.
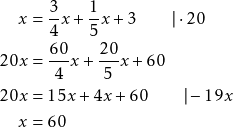
(5) Tarkastetaan tulos.
![]()
Vastaus
Kaloja saadaan 60 kpl.
Suoraan ja kääntäen verrannolliset suureet
Kaksi toisistaan riippuvaa suuretta ovat suoraan verrannolliset, jos ne muuttuvat samassa suhteessa.
Esim. 10
Aterian verollinen hinta on 4,5 €. Laske veroton hinta, kun arvonlisävero on 14 %.
Ratkaisu
Muodostetaan seuraava taulukko.

Kerrotaan taulukon alkiot ristiin, jolloin saadaan
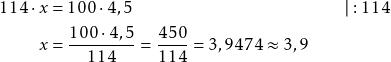
Vastaus
Veroton hinta on noin 3,9 €.
Kaksi toisistaan riippuvaa suuretta ovat kääntäen verrannolliset, jos ne muuttuvat käänteisessä suhteessa.
Esim. 11
Junan keskinopeus on 80 km/h, jolloin matka-aika on 2,5 h. Laske aika, kun keskinopeus on 100 km/h.
Ratkaisu
Muodostetaan seuraava taulukko.

Kerrotaan taulukon alkiot suoraan, jolloin saadaan
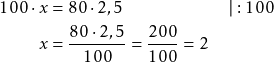
Vastaus
Matka-aika on 2 h.
Suureyhtälöt
Suureyhtälö (yhtälö, kaava) kertoo suureiden välisen riippuvuuden.
Matematiikan, fysiikan ja/tai kemian laskuissa (1) kerää suureiden arvot, (2) ratkaise suureyhtälöstä oikea suure, (3) sijoita yhtälöön tunnetut arvot yksiköineen, (4) pyöristä vastaus lähtöarvojen perusteella ja (5) kirjoita vastaus yksiköineen.
Esim. 12
Laske matka-aika, kun 280 km matkan keskinopeus on 80,0 km/h.
Ratkaisu
(1) Kerätään alkuun annetut suureet arvoineen.
![]()
(2) Ratkaistaan keskinopeuden suureyhtälöstä ![]() matka-aika.
matka-aika.
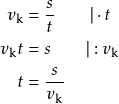
(3) Sijoitetaan tunnetut arvot.
![Rendered by QuickLaTeX.com \[ t = \frac{280\;\text{km}}{80,0\;\dfrac{\text{km}}{\text{h}}} = 3,5\;\text{h} \]](https://blogit.gradia.fi/matvalinnainen/wp-content/ql-cache/quicklatex.com-74fc891bd4fa8ced98f561bcc61f3b14_l3.png)
(4) Koska matka on ilmaistu kahdella merkitsevällä numerolla ja nopeus kolmella, ilmoitetaan vastaus epätarkimman mukaisesti.
(5) Vastaus
Matka aika on 3,5 h.
Fysiikan laskuissa välituloksia ei pyöristetä, mutta välituloksen yksiköt merkitään.
Kirjoitetaan vielä koonti suureyhtälöiden ratkaisuvaiheista.
Suureyhtälö 1
Kertoimesta pääsee eroon jakamalla.
Esim. 13
Ratkaise ![]() .
.
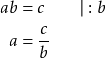
Suureyhtälö 2
Jakajasta pääsee eroon kertomalla.
Esim. 14
Ratkaise ![]() .
.
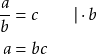
Suureyhtälö 3
Jos ratkaistava suure on väärällä puolella, vaihdetaan järjestys.
Esim. 15
Ratkaise ![]() .
.
![]()
Suureyhtälö 4
Jos ratkaistava suure on jakajana, kerrotaan molemmat puolet kyseisellä jakajalla.
Esim. 16
Ratkaise ![]() .
.
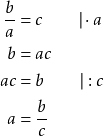
Suureyhtälö 5
Jos ratkaistava suure on toisessa potenssissa, otetaan molemmilta puolilta neliöjuuri.
Esim. 17
Ratkaise ![]() .
.
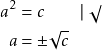
Suureyhtälö 6
Jos ratkaistava suure on neliöjuuressa, korotetaan molemmat puolet toiseen potenssiin.
Esim. 18
Ratkaise ![]() .
.
![]()
Toisen asteen yhtälöt
Kirjoitetaan toisen asteen yhtälön yleinen muoto.
![]()
Edellisen yhtälön ratkaisut eli juuret ovat funktion ![]() nollakohdat.
nollakohdat.


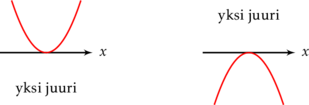
Esim. 19
Kanalan seinän viereen rakennetaan aitaus, jonka kolmeen sivuun on käytettävissä 8 metriä aitaa. Kanalan seinää vastaan kohtisuoran sivun pituus on ![]() metriä.
metriä.
(1) Piirretään kuvio ja ilmaistaan seinän suuntaisen sivun pituus muuttujan ![]() lausekkeena.
lausekkeena.
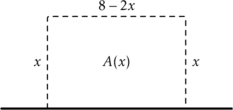
(2) Ilmaistaan aitauksen pinta-ala muuttujan ![]() funktiona
funktiona ![]() .
.
![]()
(3) Lasketaan funktion ![]() arvot muuttujan
arvot muuttujan ![]() arvoilla 0, 1, 2, 3 ja 4 ja piirretään funktion kuvaaja.
arvoilla 0, 1, 2, 3 ja 4 ja piirretään funktion kuvaaja.
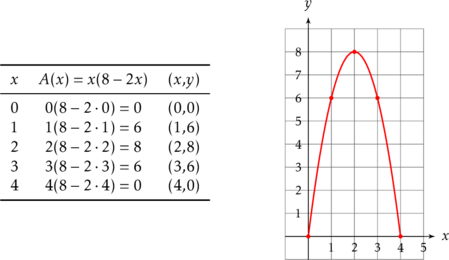
Aitauksen pinta-ala (eli funktion ![]() huippu) on suurin, kun
huippu) on suurin, kun ![]() . Pinta-alan maksimi on
. Pinta-alan maksimi on ![]() .
.
Jos toisen asteen yhtälössä ![]() termi
termi ![]() , on yhtälö seuraavaa muotoa.
, on yhtälö seuraavaa muotoa.
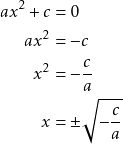
Yhtälöllä on kaksi juurta.
![]()
Jos termi ![]() , ei yhtälöllä ole juuria.
, ei yhtälöllä ole juuria.
Esim. 20
Ratkaise ![]() .
.
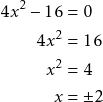
Kirjoitetaan yhtälön ratkaisut.
![]()
Jos toisen asteen yhtälössä ![]() termit
termit ![]() ja
ja ![]() , on yhtälö seuraavaa muotoa.
, on yhtälö seuraavaa muotoa.
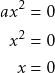
Yhtälön juuri on ![]() .
.
Esim. 21
Ratkaise ![]() .
.
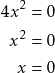
Yhtälön juuri on ![]() .
.
Jos toisen asteen yhtälössä ![]() termi
termi ![]() , on yhtälö seuraavaa muotoa.
, on yhtälö seuraavaa muotoa.
![]()
Yhtälö on nolla, jos jompi kumpi tulon tekijöistä on nolla.
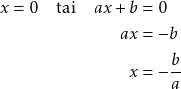
Kirjoitetaan yhtälön ratkaisut.
![]()
Esim. 22
Ratkaise ![]() .
.
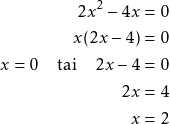
Kirjoitetaan yhtälön ratkaisut.
![]()
Kirjoitetaan toisen asteen yhtälön ![]() ratkaisukaava.
ratkaisukaava.

Esim. 23
Ratkaise ![]() .
.
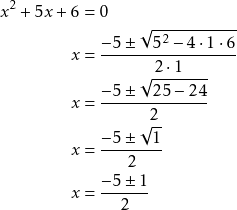
Kirjoitetaan yhtälön ratkaisut.
![]()
Esim. 24
Ratkaise ![]() .
.
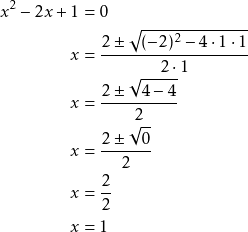
Yhtälön ratkaisu on ![]() .
.
Esim. 25
Ratkaise ![]() .
.
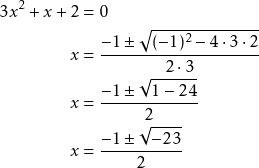
Yhtälöllä ei ole reaaliratkaisua, koska ![]() ei ole reaaliluku.
ei ole reaaliluku.
Yhtälöparit
Yhtälöparissa on merkintänä yleensä aaltosulje. Siinä on kaksi kahden muuttujan yhtälöä. Muuttujien arvot toteuttavat yhtälöparin, jos ne toteuttavat molemmat yhtälöparin yhtälöt.
Yhteenlaskumenetelmässä (1) yhtälöt kerrotaan sopivasti siten, että toisen muuttujan kertoimet ovat vastaluvut, (2) yhtälöt lasketaan yhteen, jolloin ratkaistavaksi jää vain yhtälö, jossa on yksi muuttuja, (3) saatu ratkaisu sijoitetaan jompaankumpaan yhtälöpareista ja (4) toisen muuttujan arvo ratkaistaan yhteenlaskumenettelyllä.
Esim. 26
Määritä yhteenlaskumenetelmällä ne luvut ![]() ja
ja ![]() , jotka toteuttavat molemmat yhtälöt
, jotka toteuttavat molemmat yhtälöt ![]() ja
ja ![]() .
.
Ratkaisu
Kirjoitetaan yhtälöpari.
![]()
(1) + (2) Ratkaistaan yhtälöpari poistamalla toinen tuntematon, jolloin saadaan yksi yhden tuntemattoman yhtälö.
![Rendered by QuickLaTeX.com \[\TABbinary \tabularLongunderstack{rrll}{ 2x & - 3y = & -1 & \\ \manybrak[] -x & + y = & 3 \qquad\qquad & \vert \cdot 3 \\ & & & \\ 2x & - 3y = & -1 & \\ \manybrak[]\xlu{-3x} & \xlu{{}+ 3y =} & \xlu{9} & \\ -x & = & 8 \qquad\qquad & \vert \cdot (-1) \\ & x = & -8 & } \]](https://blogit.gradia.fi/matvalinnainen/wp-content/ql-cache/quicklatex.com-7fc6f3cb91a95c9e833088e202b37ab8_l3.png)
(3) + (4) Ratkaistaan ![]() -koordinaatti sijoittamalla
-koordinaatti sijoittamalla ![]() jompaankumpaan alkuperäisistä yhtälöistä.
jompaankumpaan alkuperäisistä yhtälöistä.
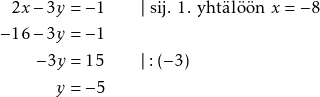
Molemmat yhtälöt toteuttavat luvut ovat ![]() ja
ja ![]() .
.
Vastaus
![]() ja
ja ![]()
Yhtälöpari voidaan ratkaista myös sijoitusmenetelmällä.
Esim. 27
Ratkaise sijoitusmenetelmällä yhtälöpari.
![]()
Ratkaisu
Sijoitetaan jälkimmäiseen yhtälöön ensimmäisen yhtälö, jossa ![]() on ilmaistu
on ilmaistu ![]() :n lausekkeena.
:n lausekkeena.
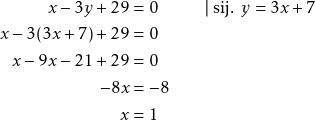
Sijoitetaan ![]() ensimmäiseen yhtälöön
ensimmäiseen yhtälöön ![]() .
.
![]()
Vastaus
![]() ja
ja ![]()
Yhtälöparien sovelluksia
Esim. 28
Matti ja Maija saivat lahjaksi yhteensä 205 € siten, että Maija sai 85 € enemmän kuin Matti. Laske lahjojen suuruudet.
Ratkaisu
Olkoon Matin saama raha ![]() ja Maijan
ja Maijan ![]() .
.
Kirjoitetaan rahojen summa.
![]()
Kirjoitetaan rahojen erotus.
![]()
Muodostetaan ja ratkaistaan yhtälöpari.
![Rendered by QuickLaTeX.com \[\TABbinary \tabularLongunderstack{rrll}{ x & + y = & 205 & \\ \manybrak[]\xlu{x} & \xlu{{}- y =} & \xlu{-85} & \\ 2x & = & 120 \qquad\qquad & \vert : 2 \\ & x = & 60 & \\ & & & \\ x & - y = & -85 & \vert ~ x = 60 \\ & y = & 145 & } \]](https://blogit.gradia.fi/matvalinnainen/wp-content/ql-cache/quicklatex.com-6829ef700453e0adb9d2a57c9e5ffdd2_l3.png)
Vastaus
Matti sai 60 € ja Maija sai 145 €.
Esim. 29
Astiassa on vettä, jonka sokeripitoisuus 4 %. Toisessa astiassa veden sokeripitoisuus on 14 %. Laske sekoitussuhde, kun halutaan kaksi litraa vettä, jonka sokeripitoisuus on 7 %.
Ratkaisu
Olkoon vesimäärät ![]() ja
ja ![]() .
.
Kirjoitetaan summa.
![]()
Pitoisuudet määräytyvät yhtälöstä
![]()
Muodostetaan ja ratkaistaan yhtälöpari.
![Rendered by QuickLaTeX.com \[\TABbinary \tabularLongunderstack{rrll}{ x & + y = & 2 & \vert \cdot (-0,04) \\ \manybrak[]0,04x & + 0,14y = & 0,14 & \\ & & & \\ -0,04x & - 0,04y = & -0,08 & \\ \manybrak[]\xlu{\quad 0,04x} & \xlu{{}+ 0,14y =} & \xlu{0,14} & \\ & 0,10y = & 0,06 \qquad & \vert : 0,10 \\ & y = & 0,6 & \\ & & & \\ x & + y = & 2 & \vert ~ y = 0,6 \\ & x = & 1,4 & } \]](https://blogit.gradia.fi/matvalinnainen/wp-content/ql-cache/quicklatex.com-6bebef1bc15f7853fa5943eb927f62f9_l3.png)
Vastaus
Ensimmäisestä astiasta otetaan 1,4 litraa ja toisesta 0,6 litraa.