Verrantoa voidaan käyttää monenlaisten ongelmien ratkaisussa:
- matkaan käytetty aika ja nopeus
- tavaran määrä ja hinta
- verotettavan tulon ja veron määrä
- työaika ja työpalkka
- muuntajan jännite ja käämin kierrosluku
A) Esimerkkejä verrannon ratkaisemisesta
Ratkaise verrantomuotoiset yhtälöt.
Esim. 1
![]()
Kerrotaan ”ristiin” verrantoyhtälön vasemmalta ylhäältä ![]() ja oikealta alhaalta 21. Samoin 7 ja 6.
ja oikealta alhaalta 21. Samoin 7 ja 6.
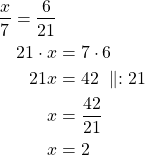
Vastaus: ![]() .
.
Esim. 2
![]()
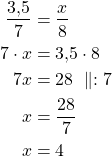
Vastaus: ![]() .
.
B) Verrannon muodostaminen
Suoraan verrannollisuus
Suureet ovat suoraan verrannollisia, kun ne suurenevat tai pienenevät samassa suhteessa.
Esim. 3 Jos 3 kg perunaa maksaa 2,25 €, kuinka paljon maksaa 5 kg perunaa?
Laaditaan tiedoista taulukko. Merkitään tuntematonta hintaa ![]() :llä.
:llä.
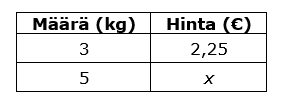
Kirjoitetaan ja ratkaistaan verrantoyhtälö:
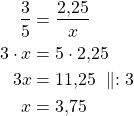
Vastaus: 5 kg perunoita maksaa 3,75 €.
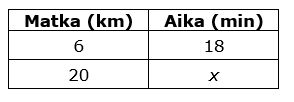
Esim. 4 Seppo pyöräili 6 kilometrin matkan 18 minuutissa. Kuinka kauan kestäisi 20 kilometrin matka samalla nopeudella?
Laaditaan tiedoista taulukko. Merkitään tuntematonta aika ![]() :llä.
:llä.
Kirjoitetaan ja ratkaistaan verrantoyhtälö:
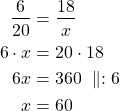
Vastaus: 20 kilometrin matka kestää 60 minuuttia eli 1 h.
Kääntäen verrannollisuus
Suureet ovat kääntäen verrannollisia, kun toisen kasvaessa toinen pienenee samassa suhteessa. Verranto ratkaistaan kääntämällä toinen suhteista.
Esim. 5 Matkaan opiskelupaikkakunnalta kotiin kuluu autolla 1 h 25 min, jos keskinopeus on 80 km/h. Kuinka kauan matka kestäisi, jos keskinopeus olisi huonon ajokelin takia 70 km/h?
1 h 25 min = 60 min + 25 min = 85 min.
Laaditaan tiedoista taulukko. Merkitään tuntematonta aikaa ![]() :llä.
:llä.

Käännetään toinen suhteista ylösalaisin. Kirjoitetaan ja ratkaistaan verrantoyhtälö:
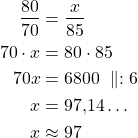
Voidaan ilmoittaa aika 97 minuuttia tunteina ja minuutteina: 97 min = 1 h 37 min.
Vastaus: Matka kestää 97 minuuttia eli 1 h 37 min.