Ensimmäisen asteen yhtälöt - Yhtälöiden osaaminen

Tehtävät

Ratkaisusäännöt:

Poista sulut (jos niitä on).
Poista nimittäjät eli jakajat (jos niitä on).
Siirrä kaikki tuntemattoman sisältämän termit (yleensä 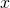$x$ :t) samalle puolelle yhtäsuuruusmerkkiä (yleensä vasemmalle) ja muut toiselle puolelle (yleensä oikealle). Siirrettäessä termejä puolelta toiselle niiden etumerkki muuttuu.
Yhdistä termit, joissa on sama kirjainosa.
Ratkaise kuten tekijäyhtälö.
Tarkista ratkaisu.

Merkkisäännöt kerto- ja jakolaskussa

$+ \cdot + = +$
$+ \cdot - = -$
$- \cdot + = -$
$- \cdot - = +$

Esimerkkejä yhtälöiden mekaanisesta ratkaisemisesta

Esim. 1 Ratkaise yhtälö $4x-13=2x-7$ .

$\begin{align*}4x - 13 &= 2x - 7\\4x - 2x &= -7 + 13\\2x &=6\ \parallel :2\\x &=\frac{6}{2}\\x &= 3\end{align*}$

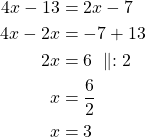
Tarkistus: Sijoitetaan alkuperäisen yhtälön vasemmalle ja oikealle puolelle $x=3$ .

Vasen puoli: $4 \cdot 3 -13 = 12-13=-1$

Oikea puoli: $2 \cdot 3 - 7 = 6-7 = -1$

Yhtälö on ratkaistu oikein.

Vastaus: $x=3$ .

Esim. 2 Ratkaise yhtälö $3(x + 2) = x + 2$ .

$\begin{align*}3(x + 2) &= x + 2\\3 \cdot x + 3 \cdot 2 &= x+2\\3x +6&=x+2\\3x-x &=2-6\\2x &=-4\ \parallel:2\\x &= \frac{-4}{2} \\x &= -2\end{align*}$

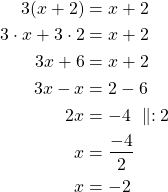
Vastaus: $x = -2$ .

Esim. 3 Ratkaise yhtälö $7(2 + x) - 3(x - 2) - 28 = 2x - 4(-2x + 4)$ .

$\begin{align*}7(2 + x) - 3(x - 2) - 28 &= 2x - 4(-2x + 4)\\7 \cdot 2 + 7 \cdot x -3 \cdot x -3 \cdot (-2) -28 &= 2x -4 \cdot(-2x) -4 \cdot 4\\14 + 7x -3x + 6 - 28 &= 2x + 8x - 16\\7x -3x -2x -8x &=-16 - 14 - 6 + 28\\-6x &=-8\ \parallel:(-6)\\x &= \frac{-8}{-6} \\x &= \frac{4}{3}\\x &= 1 \frac{1}{3}\end{align*}$

Vastaus: $x = 1 \dfrac{1}{3}$ .

Esimerkkejä yhtälöiden muodostamisesta

Kirjoita yhtälöt ja ratkaise.

Esim. 4 Kun eräs luku kerrotaan kolmella ja tuloon lisätään 5, saadaan 23. Mikä on kysytty luku?

Merkitään kysyttä lukua $x$ :llä.

$\begin{align*}x \cdot 3 + 5 &=23\\3x + 5 &=23\\3x &= 23-5\\3x &= 18\\x &= \frac{18}{3}\\x &= 6\end{align*}$

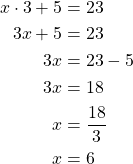
Tarkistus: $6 \cdot 3 + 5 = 18 + 5 = 23$ .

Vastaus: Kysytty luku on 6.

Esim. 5 Seppo ja Markku saivat palkkaa siivouksesta yhteensä 48 €. Markku sai 5 euroa enemmän kuin Seppo. Kuinka paljon kumpikin saivat palkkaa?

Merkitään Sepon saamaa palkkaa $x$ (€). Tällöin Markku saa $x + 5$ (€).

Muodostetaan yhtälö.

$\begin{align*}x + (x + 5) &=48\\x + x+ 5 &=48\\2x &= 48-5\\2x &= 43\\x &= \frac{43}{2}\\x &= 21{,}50\end{align*}$

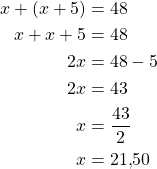
Markun saaman palkan suuruus on $21{,}50 + 5 = 26{,}50$ (€).

Yhteensä 21,50 € + 26,50 € = 48,00 €.

Vastaus: Seppo saa 21,50 € ja Markku 26,50 €.

Esim. 6 Tiina on säästänyt yhteensä 460 €. Hänen rahansa ovat 10 ja 20 euron seteleinä. Kuinka monta 10 ja 20 euron seteliä hänellä on, kun seteleitä on yhteensä 25 kappaletta?

Merkitään 10 euron seteleiden lukumäärää $x$ (kpl). Tällöin 20 euron seteleiden lukumäärä on $25-x$ (kpl).

Muodostetaan yhtälö:

$\begin{align*}10 \cdot x + 20 \cdot (25 -x) &=460\\10x + 20 \cdot 25 - 20 \cdot x &= 460\\10x + 500 - 20x &= 460\\-10 x &= 460 - 500\\-10 x &= -40\ \parallel (-10)\\x &= \frac{-40}{-10}\\x &= 4\end{align*}$

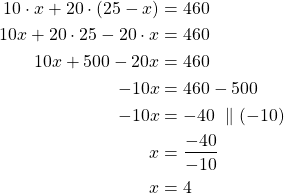
20 euron seteleiden lukumäärä on $25-4 = 21$

Tarkistetaan:

10 euron seteleistä tulee $4 \cdot 10$ € $= 40$ (€).

20 euron seteleistä tulee $21 \cdot 20$ € $= 420$ (€).

Yhteensä 460 €.

Vastaus: 10 euron seteleitä on 4 kpl ja 20 euron seteleitä 21 kpl.