Tilavuudet

1 Suorakulmainen särmiö

Rendered by QuickLaTeX.com

Suorakulmiaisen särmiön tilavuus V saadaan kertomalla pohjan pinta-ala korkeudella. Koska pohjan pinta-ala on suorakulmion pinta-ala, niin nämä voidaan kirjoittaa seuraavasti:

    \[ \boxed{ V=A_\text{p}h=abh }\]

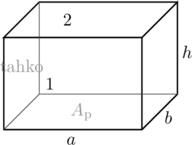
Suorakulmiaisen särmiön vaipan pinta-ala saadaan laskemalla kaikkien sivutahkojen pinta-alat yhteen. Yksi sivutaho on suorakulmion muotoinen.

    \[ \boxed{ A=2\cdot ab+ 2\cdot ah+2 \cdot bh }\]

2 Kuutio

Kuutio on suorakulmaisen särmiön erikoistapaus, jonka kaikki sivut ovat yhtä pitkiä.

Rendered by QuickLaTeX.com

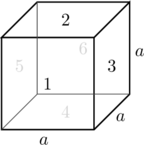
Kuution tilavuus on

    \[ \boxed{ V=A_\text{p}a=(a\cdot a)\cdot a=a^3 }\]

Kuution vaipan pinta-ala on

    \[ \boxed{ A=6\cdot a\cdot a=6a^2 }\]

3 Lieriö

Piirretään ympyräpohjainen suora lieriö, jonka säde on r ja korkeus h.

Rendered by QuickLaTeX.com

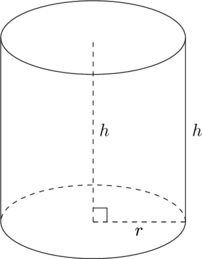
Lieriön tilavuus on

    \[ \boxed{ V=\pi r^2 h }\]

Lieriön vaipan ala on

    \[ \boxed{ A_\text{V}=2\pi r h }\]

4 Kartio

Piirretään ympyräpohjainen suora lieriö. Pohjaympyrän säde on r. Kartion korkeus h on kohtisuorassa sädettä vastaan. Kartion sivun pituus on s.

Rendered by QuickLaTeX.com

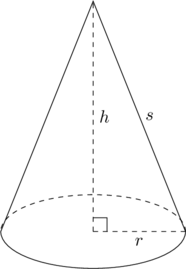
Kartion tilavuus on

    \[ \boxed{ V=\frac{\pi r^2 h}{3} }\]

5 Pallo

Rendered by QuickLaTeX.com

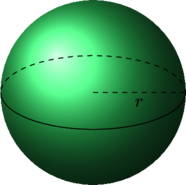
Pallon tilavuus on

    \[ \boxed{ V=\frac{4}{3}\pi r^3 }\]

Pallon pinta-ala on

    \[ \boxed{ A=4\pi r^2 }\]