Pythagoraan lause - Geometrian osaaminen

Suorakulmaisen kolmion tapauksessa kolmion sivujen pituuksien neliöt noudattavat Pythagoraan lausetta.

Piirretään suorakulmainen kolmio, jonka kateetit ovat $a$ ja $b$ . Kateetit ovat kohtisuorassa toisiaan vastaan. Merkitään kolmion pisintä sivua, hypotenuusaa, kirjaintunnuksella $c$ .

Rendered by QuickLaTeX.com

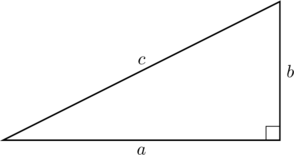
Pythagoraan lauseen mukaan suorakulmaisen kolmion kateettien neliöiden summa on hypotenuusan neliö. Neliö tarkoittaa sivun pituuden toista potenssia.

$\boxed{a^2+b^2=c^2}$

Esimerkki 1

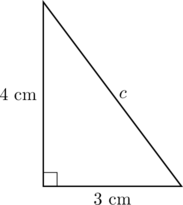
Laske suorakulmaisen kolmion hypotenuusan pituus, kun kateetit ovat 3 cm ja 4 cm.

Suorakulmaisen kolmion sivun pituuden ratkaisemisessa Pythagoraan lauseen avulla ei sisänsä ole väliä, millä kirjaintunnuksella merkitään mitäkin sivua. Merkitään hypotenuusan pituutta kirjaintunnukslla $c$ . Piirretään suorakulmainen kolmio vähän eri asentoon kuin teorian esimerkkikuviossa.

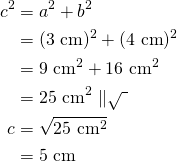
Rendered by QuickLaTeX.com

$\begin{align*}c^2&=a^2+b^2\\&=(3\ \text{cm})^2+(4\ \text{cm})^2\\&=9\ \text{cm}^2+16\ \text{cm}^2\\&=25\ \text{cm}^2\ \|\sqrt{\ }\\c&=\sqrt{ 25\ \text{cm}^2 }\\&=5\ \text{cm}\end{align*}$

Vastaus: Hypotenuusan pituus on $5\ \text{cm}$ .

Esimerkki 2

Laske suorakulmaisen kolmion kateetin pituus, kun hypotenuusan pituus on 3,5 m ja toisen kateetin pituus on 1,2 m.

Merkitään toisen kateetin pituutta $x$ (m). Piirretään suorakulmainen kolmio.

Rendered by QuickLaTeX.com

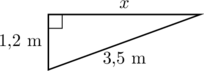
Kirjoitetaan Pythagoraan lause tässä esimerkissä seuraavasti:

$\begin{align*}x^2+(1{,}2\ \text{m})^2&=(3{,}5\ \text{m})^2\\x^2+1{,}44\ \text{m}^2&=12{,}25\ \text{m}^2\\x^2&= 12{,}25\ \text{m}^2 - 1{,}44\ \text{m}^2 \\x^2&= 10{,}81\ \text{m}^2\ \|\sqrt{\ }\\x&=\sqrt{ 10{,}81\ \text{m}^2 }\\&=3{,}28756\ \text{m}\\&\approx 3{,}3\ \text{m}\end{align*}$

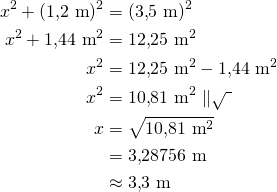
Vastaus: Kateetin pituus on $3{,}3\ \text{m}$ .