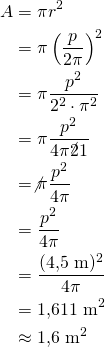Piiri ja pinta-ala - Geometrian osaaminen

Tehtävät

Piiriä merkitään kirjaintunnuksella $p$ . Se tarkoittaa jonkin kuvion ympärysmittaa.
Pinta-alaa merkitään kirjaintunnuksella $A$ .

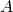1 Suorakulmio

Piirretään suorakulmio, jonka sivut ovat $a$ ja $b$ .

Rendered by QuickLaTeX.com

Suorakulmion piiri on

$\boxed{ p=2a + 2b }$

Suorakulmion pinta-ala on

$\boxed{A=ab}$

Esimerkki 1

Suorakulmion sivujen pituudet ovat $4{,}0\ \text{cm}$ ja $3{,}0\ \text{cm}$ . Laske suorakulmion
a) piiri,
b) pinta-ala.

a) Piiri on

$\begin{align*}p&=2a+2b\\&=2 \cdot 4{,}0\ \text{cm}+2 \cdot 3{,}0\ \text{cm}\\&=8{,}0\ \text{cm}+6{,}0\ \text{cm}\\&=14{,}0\ \text{cm}\end{align*}$

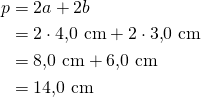
b) Pinta-ala on

$\begin{align*}A&=a \cdot b\\&= 4{,}0\ \text{cm} \cdot 3{,}0\ \text{cm}\\&=12\ \text{cm}^2\end{align*}$

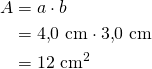
2 Kolmio

Piirretään kolmio, jonka kantasivu on $a$ ja korkeus $h$ .

Rendered by QuickLaTeX.com

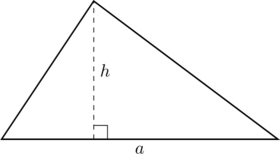
Kolmion pinta-ala on

$\boxed{A=\frac{ah}{2}}$

Esimerkki 2

Kolmion kantasivun pituus on $6{,}0\ \text{cm}$ ja korkeus $3{,}0\ \text{cm}$ . Laske kolmion pinta-ala.

$\begin{align*}A&=\frac{ab}{2}\\&=\frac{ 6{,}0\ \text{cm} \cdot 3{,}0\ \text{cm} }{2}\\&=9{,}0\ \text{cm}^2\end{align*}$

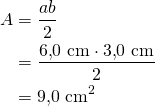
3 Suunnikas

Suunnikkaan vastakkaiset sivut ovat yhdensuuntaiset.

Piirretään suunnikas, jonka kantasivu on $a$ ja korkeus $h$ .

Rendered by QuickLaTeX.com

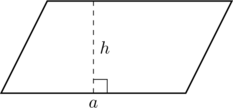
Suunnikkaan pinta-ala on

$\boxed{A=ah}$

Esimerkki 3

Suunnikkaan kantasivun pituus on $5{,}2\ \text{cm}$ ja korkeus $3{,}5\ \text{cm}$ . Laske suunnikkaan pinta-ala.

$\begin{align*}A&=ah\\&=5{,}2\ \text{cm} \cdot 3{,}5\ \text{cm}\\&=18{,}2\ \text{cm}^2\\&\approx 18\ \text{cm}^2 \end{align*}$

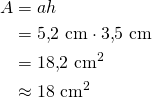
4 Puolisuunnikas

Puolisuunnikkaan toiset vastakkaiset sivut ovat yhdensuuntaiset ja toiset vastakkaiset sivut erisuuntaiset.

Piirretään puolisuunnikas, jonka kaksi yhdensuuntaista sivua ovat $a$ ja $b$ . Sivua $a$ eli kantaa vastaan kohtisuorassa on korkeus $h$ .

Rendered by QuickLaTeX.com

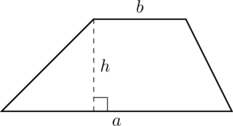
Puoliuunnikkaan pinta-ala on

$\boxed{A=\frac{a+b}{2}\cdot h}$

Esimerkki 4

Puolisuunnikkaan yhdensuuntaiset sivut ovat $50\ \text{m}$ ja $60\ \text{m}$ sekä korkeus on $20\ \text{m}$ . Laske puolisuunnikkan ala.

$\begin{align*}A&=\frac{a+b}{2}\cdot h\\&=\frac{ 50\ \text{m}+ 60\ \text{m}}{2}\cdot 20\ \text{m} \\&=1100\ \text{m}^2\end{align*}$

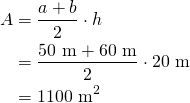
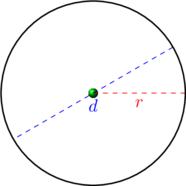
5 Ympyrä

Ympyrä on niiden tason pisteiden joukko, jotka ovat säteen etäisyydellä ympyrän keskipisteestä.

Säteen kirjaintunnus on $r$ . Halkaisijan kirjaintunnus on $d$ .

$\pi$ (eli pii) tarkoittaa ympyrän kehän pituuden (eli piirin eli ympärysmitan) suhdetta halkaisijaan. Piin likiarvo on $3{,}14$ .

Rendered by QuickLaTeX.com

Ympyrän piiri on

$\boxed{p=2\pi r}$

Ympyrän pinta-ala on

$\boxed{A=\pi r^2}$

Esimerkki 5

Ympyrän halkaisija on $10\ \text{cm}$ . Laske säde, piiri ja pinta-ala.

Säde on $r=\dfrac{10\ \text{cm}}{2}=5{,}0\ \text{cm}$ .

Piiri on $p=2\pi r=2 \cdot \pi \cdot 5{,}0\ \text{cm}=31{,}4\ \text{cm}\approx 31\ \text{cm}$ .

Pinta-ala on $A=\pi r^2 = \pi \cdot (5{,}0\ \text{cm})^2=78{,}5398\ \text{cm}^2 \approx 79\ \text{cm}^2$ .

Esimerkki 6

Ympyrän muotoisen pöydän piiri on 4,5 m.
a) Laske pöydän säde?
b) Laske pöydän pinta-ala?

a) Ratkaistaan piirin yhtälöstä säde $r$ .

$\begin{align*}p&=2 \pi r\\2 \pi r&= p\ \|:(2\pi)\\r&=\frac{p}{2\pi}\\&=\frac{4{,}5\ \text{m}}{2 \pi}\\&=0{,}7162\ \text{m}\\&\approx 0{,}72\ \text{m}\end{align*}$

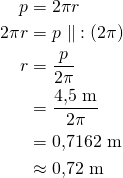
b) Pinta-ala on

$\begin{align*}A&=\pi r^2\\&=\pi (0{,}7162\ \text{m})^2\\&=1{,}611\ \text{m}^2\\&\approx 1{,}6\ \text{m}^2\end{align*}$

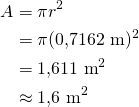
Huom! Ratkaistaan ympyrän pinta-ala ilman, että ensin on ratkaistu pöydän säde.

Edellä saatiin, että pöydän säde on piirin avulla lausuttuna

$r=\frac{p}{2\pi}$

Sijoitetaan säteen lauseke pinta-alan lausekkeessa $r$ :n tilalle. Tällöin saadaan

$\begin{align*}A&=\pi r^2\\&=\pi \left(\frac{p}{2\pi}\right)^2\\&=\pi \frac{p^2}{2^2 \cdot \pi^2}\\&=\pi \frac{p^2}{4\pi^\not{2}1}\\&=\not{\pi}\frac{p^2}{4\pi}\\&=\frac{p^2}{4\pi}\\&=\frac{(4{,}5\ \text{m})^2}{4\pi}\\&= 1{,}611\ \text{m}^2\\&\approx 1{,}6\ \text{m}^2 \end{align*}$