Mittakaava

Tehtävät

Mittakaava tarkoittaa suhdetta esimerkiksi piirroksessa olevan mitan ja todellisen kohteen mitan välillä.

Esimerkki 1 a

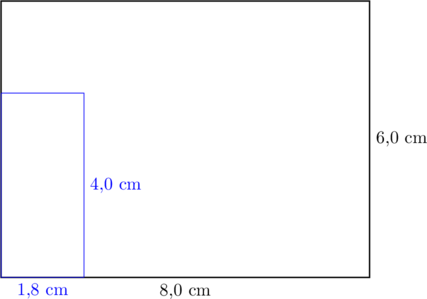
Piirretään huone, jonka seinien mitat piirroksessa ovat 8,0 cm ja 6,0 cm.

Rendered by QuickLaTeX.com

Piirroksen ja todellisen huoneen mittojen välinen suhde(luku) on 1:50. Se tarkoittaa sitä, että piirroksesta mitattu mitta on todellisuudessa 50 kertaa suurempi.

Huoneen seinien mitat todellisuudessa ovat
50 \cdot 8{,}0\ \text{cm} =400\ \text{cm} =4{,}0\ \text{m}
50 \cdot 6{,}0\ \text{cm} =300\ \text{cm} =3{,}0\ \text{m}

Esimerkki 1 b

Lasketaan huoneen pinta-ala sekä piirroksessa että todellisuudessa.

Pinta-ala piirroksesssa on

    \[A= 8{,}0\ \text{cm} \cdot 6{,}0\ \text{cm} = 48\ \text{cm}^2\]

Pinta-ala todellisuudessa on

    \[A= 4{,}0\ \text{m} \cdot 3{,}0\ \text{m} = 12\ \text{m}^2\]

Esimerkki 1 c

Piirretään seuraavaksi huoneeseen sänky, jonka mitat todellisuudessa ovat 90 cm x 200 cm.

Muutetaan mitat todellisuudesta piirrokseen jakamalla sängyn mitat 50:llä, koska piirroksen mittakaava on 1:50.

Sängyn mitat piirroksessa ovat

90\ \text{cm} :50 =1{,}8\ \text{cm}
200\ \text{cm} :50 =4{,}0\ \text{cm}

Rendered by QuickLaTeX.com

Esimerkki 1 d

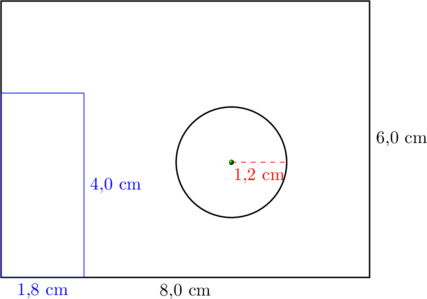
Huoneessa on halkaisijaltaan 1,2 metrin mittainen pöytä. Laske pöydän piiri ja pinta-ala. Piirretään pöytä piirustukseen.

Halkaisijasta saadaan säde r=\dfrac{1{,}2\ \text{m}}{2}=0{,}60\ \text{m}=60\ \text{cm}.
Säteen mitta piirroksessa on r= 60\ \text{cm} : 50=1{,}2\ \text{cm}.

Rendered by QuickLaTeX.com

Pöydän piiri (eli ympärysmitta eli kehän pituus) on

    \[p=2\pi r=2 \pi \cdot 0{,}60\ \text{m} =3{,}7699\ \text{m} \approx 3{,}8\ \text{m}\]

Pöydän pinta-ala on

    \[A=\pi r^2=\pi \cdot (0{,}60\ \text{m} )^2=1{,}13097\ \text{m}^2 \approx 1{,}1\ \text{m}^2\]