1 Suorakulmainen särmiö
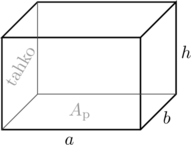
Suorakulmiaisen särmiön tilavuus ![]() saadaan kertomalla pohjan pinta-ala korkeudella. Koska pohjan pinta-ala on suorakulmion pinta-ala, niin nämä voidaan kirjoittaa seuraavasti:
saadaan kertomalla pohjan pinta-ala korkeudella. Koska pohjan pinta-ala on suorakulmion pinta-ala, niin nämä voidaan kirjoittaa seuraavasti:
![]()
Suorakulmiaisen särmiön vaipan pinta-ala saadaan laskemalla kaikkien sivutahkojen pinta-alat yhteen. Yksi sivutaho on suorakulmion muotoinen.
![]()
Postipaketin koko on ![]() . Laske paketin tilavuus
. Laske paketin tilavuus
a) kuutiosenttimetreinä,
b) litroina.
Ratkaisu:
a) Paketin tilavuus on
![]()
Vastaus: Tilavuus on ![]()
b) Tilavuus muutetaan litroiksi eli kuutiodesimetreiksi jakamalla tuhannella tai siirtämällä pilkkua kolmen numeron yli vasemmalle.
![]()
Vastaus: Tilavuus on ![]() .
.
2 Kuutio
Kuutio on suorakulmaisen särmiön erikoistapaus, jonka kaikki sivut ovat yhtä pitkiä.
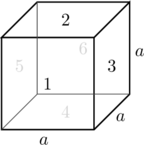
Kuution tilavuus on
![]()
Kuution vaipan pinta-ala on
![]()
Kuution vaipan pinta-ala on ![]() . Määritä kuution sivun pituus.
. Määritä kuution sivun pituus.
Ratkaisu: Yhden sivutahkon pinta-ala on
![]()
Sivun pituus saadaan ratkaistua yhden tahkon pinta-alasta:
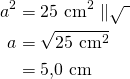
Vastaus: Sivun pituus on ![]() .
.
3 Lieriö
Piirretään ympyräpohjainen suora lieriö (vaippa on kohtisuorassa pohjaa vastaan), jonka säde on ![]() ja korkeus
ja korkeus ![]() .
.
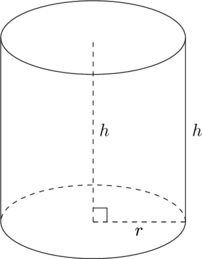
Lieriön tilavuus on
![]()
Lieriön vaipan ala on
![]()
Säilykepurkin korkeus on 9,0 cm ja halkaisija 6,0 cm. Laske säilykepurkin
a) vaipan pinta-ala,
b) tilavuus kuutiosenttimetreinä, millilitroina ja desilitroina.
Ratkaisu:
a) Säilykepurkki on suora, ympyräpohjainen lieriö, jonka pohjaympyrän säde on
![]() .
.
Vaipan pinta-ala on
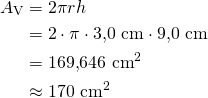
Vastaus: Vaipan pinta-ala on ![]() .
.
b) Lieriön tilavuus on
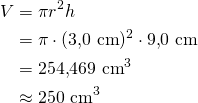
Muutetaan tilavuus millilitroiksi ja deslitroiksi:
![]()
Vastaus: Tilavuus on ![]() eli
eli ![]() eli
eli ![]() .
.
4 Kartio
Ympyräpohjaisen suoran kartion tilavuus
Piirretään ympyräpohjainen suora kartio (huipusta piirretty korkeusjanan toinen päätepiste on pohjankeskipisteessä). Pohjaympyrän säde on ![]() . Kartion korkeus
. Kartion korkeus ![]() on kohtisuorassa sädettä vastaan. Kartion sivun pituus on
on kohtisuorassa sädettä vastaan. Kartion sivun pituus on ![]() .
.
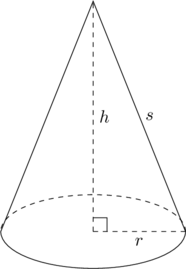
Ympyräpohjaisen suoran kartion tilavuus on
![Rendered by QuickLaTeX.com \[ \boxed{ V=\frac{\pi r^2 h}{3} }\]](https://blogit.gradia.fi/geometrianosaaminen/wp-content/ql-cache/quicklatex.com-f3147362358af30715278359bd79eb06_l3.png)
Ympyräpohjaisen suoran kartion vaipan pinta-ala
Kun kartio avataan, niin syntyvä alue on ympyräsektori, jonka kaaren pituus ![]() on sama kuin kartion pohjaympyrän piiri eli
on sama kuin kartion pohjaympyrän piiri eli ![]() .
.
Alla oleva kuva havainnollistaa tilannetta.
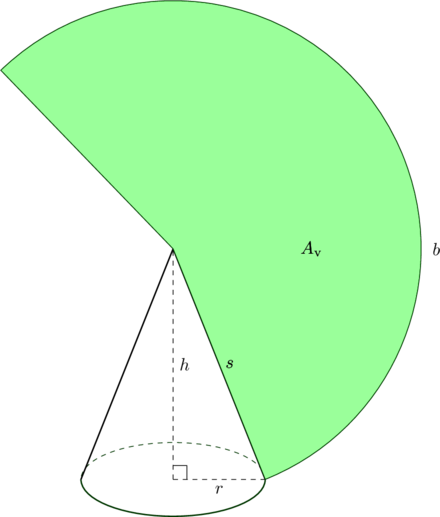
Ympyräpohjaisen suoran kartion vaipan pinta-ala on
![]()
Neliöpohjaisen suoran kartion tilavuus
Piirretään neliöpohjainen suora kartio. Pohjaneliön sivun pituus on ![]() . Kartion korkeus
. Kartion korkeus ![]() on kohtisuorassa pohjaa vastaan. Kyseessä on siis pyramidi.
on kohtisuorassa pohjaa vastaan. Kyseessä on siis pyramidi.
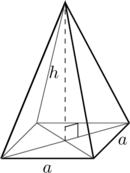
Neliöpohjaisen suoran kartion tilavuus on
![Rendered by QuickLaTeX.com \[\boxed{V=\frac{a^2h}{3}}\]](https://blogit.gradia.fi/geometrianosaaminen/wp-content/ql-cache/quicklatex.com-660be59c8cfbbe67dae419708ab1f95e_l3.png)
Neliöpohjaisen suoran kartion vaipan pinta-ala
Vaippa koostuu neljästä yhtä suuresta kolmiosta, joiden yhteenlaskettu pinta-ala on vaipan pinta-ala.
Jäätelötuutin korkeus on 11 cm ja suuaukon halkaisija on 7,0 cm. Laske tuutin tilavuus kuutiosenttimetreinä ja desilitoina.
Ratkaisu: Jäätelötuutti on ympyräpohjainen suora kartio, jonka suuaukon säde on
![]()
Tilavuus on
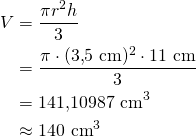
Muutetaan tilavuus desilitroiksi:
![]()
Vastaus: Tilavuus on ![]()
5 Pallo
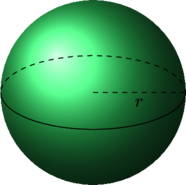
Pallon tilavuus on
![Rendered by QuickLaTeX.com \[ \boxed{ V=\frac{4\pi r^3}{3} }\]](https://blogit.gradia.fi/geometrianosaaminen/wp-content/ql-cache/quicklatex.com-51518575479c30f15957741cf6e8d575_l3.png)
Pallon pinta-ala on
![]()
Pallonmuotoisen juuston läpimitta on 9,0 cm. Tämän kokoinen juusto maksaa 5,90 €. Juuston tiheys on ![]() . Laske juustopallon
. Laske juustopallon
a) pinta-ala,
b) tilavuus,
c) massa,
d) kilogrammahinta.
Ratkaisu:
a) Juustopallon säde on puolet läpimitasta![]() .
.
Pinta-ala on
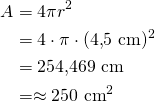
Vastaus: Pinta-ala ![]() .
.
b) Tilavuus on
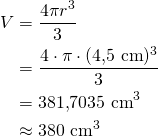
Vastaus: Tilavuus on ![]() .
.
c) Massa (![]() ) voidaan laskea tiheyden (
) voidaan laskea tiheyden (![]() ) ja tilavuuden (
) ja tilavuuden (![]() ) avulla seuraavasti:
) avulla seuraavasti:
![]()
Eli
![]()
Juustopallon massa on
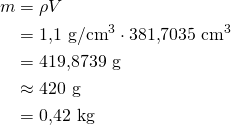
Vastaus: Juustopallon massa on ![]() .
.
d) Tuotteen kilogrammahinta lasketaan jakamalla tuotteen hinta (5,90 euroa) tuottaan massalla (0,4198739 kg).
![]()
Vastaus: Juuston kilogrammahinta on 5,90 €/kg.