Tällä sivulla on
- Tuntimuistiinpanot luvusta 2.1 tiistaina 24.8.2021
- Luku 2.1: Tehtävien 204, 210, 213, 214, 215, 216 ratkaisut.
Mukana on myös tehtävä 210, vaikka teimme sen jo tunneilla.
A – II, B – III, C – IV ja D – I
Pisteen ![]() etäisyys pisteestä
etäisyys pisteestä ![]() :
:![]()
Pisteen ![]() etäisyys pisteestä
etäisyys pisteestä ![]() :
: ![]()
Pisteen ![]() etäisyys pisteestä
etäisyys pisteestä ![]() :
: ![]()
Koska piste ![]() on ympyrällä, sen etäisyys pisteestä
on ympyrällä, sen etäisyys pisteestä ![]() on ympyrän säde.
on ympyrän säde.
Vastaus: Ympyrän säde on![]() .
.
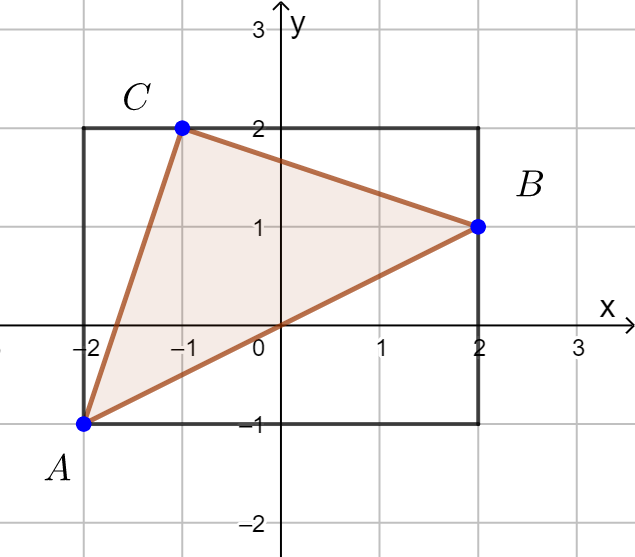
![]() ,
, ![]() ja
ja ![]()
Kolmio on tasakylkinen, jos siinä kaksi yhtä pitkää sivua. Lasketaan kolmion sivujen pituudet.
Sivun ![]() pituus on pisteiden
pituus on pisteiden ![]() ja
ja ![]() etäisyys:
etäisyys:
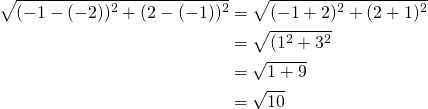
Sivun ![]() pituus on pisteiden
pituus on pisteiden ![]() ja
ja ![]() etäisyys.
etäisyys.
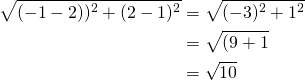
Sivun ![]() pituus on pisteiden
pituus on pisteiden ![]() ja
ja ![]() etäisyys.
etäisyys.
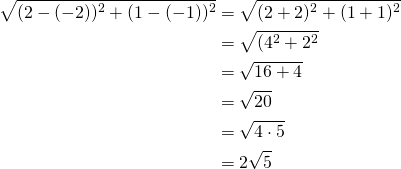
Oikeastaan sivun ![]() pituutta ei olisi tarvinnut laskea, koska tasakylkisyyden osoittamiseksi kahden sivun pituuksien tulee olla samat.
pituutta ei olisi tarvinnut laskea, koska tasakylkisyyden osoittamiseksi kahden sivun pituuksien tulee olla samat.
Koska sivut ![]() ja
ja ![]() ovat yhtä pitkät, kolmio on tasakylkinen.
ovat yhtä pitkät, kolmio on tasakylkinen.
Kannan keskipiste on janan ![]() keskipiste:
keskipiste:
![]()
Lasketaan kolmion pinta-ala vähentämällä kuvaan piirretyn suorakulmion pinta-alasta kolmen suorakulmaisen kolmion alat.
Suorakulmion pinta-ala:
Suorakulmion toisen sivun pituus on pisteiden ![]() ja
ja ![]()
![]() -koordinaattien erotuksen itseisarvo
-koordinaattien erotuksen itseisarvo
![]()
![]()
Suorakulmion pinta-ala on ![]() .
.
Suorakulmaisten kolmioiden kateettien pituudet saadaan vastaavasti koordinaattien avulla.
Suurin kolmio alhaalla:
Toinen kateetti on ![]() ja toinen
ja toinen ![]() .
.
Pinta-ala on
![]()
Ylhäällä vasemmalla oleva kolmio:
Toinen kateetti on
Pinta-ala on
![]()
Ylhäällä oikealla oleva kolmio:
Toinen kateetti on
Pinta-ala on
![]()
Siten kolmion pinta-ala on
![]()
Vastaus: Kolmion pinta-ala on ![]() .
.
Muodostetaan käyrän yhtälö annettujen ehtojen nojalla:
Pisteen ![]() -koordinaatin ja luvun
-koordinaatin ja luvun ![]() erotus on
erotus on ![]() . Tämän neliö on
. Tämän neliö on ![]() .
. ![]() -koordinaatin neliö on
-koordinaatin neliö on ![]() . Nämä ovat yhtä suuret, joten käyrän yhtälö on
. Nämä ovat yhtä suuret, joten käyrän yhtälö on
![]()
Sievennetään käyrän yhtälö:
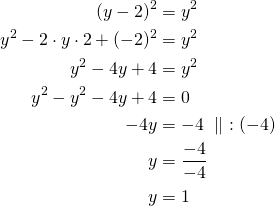
Käyrä on seuraava
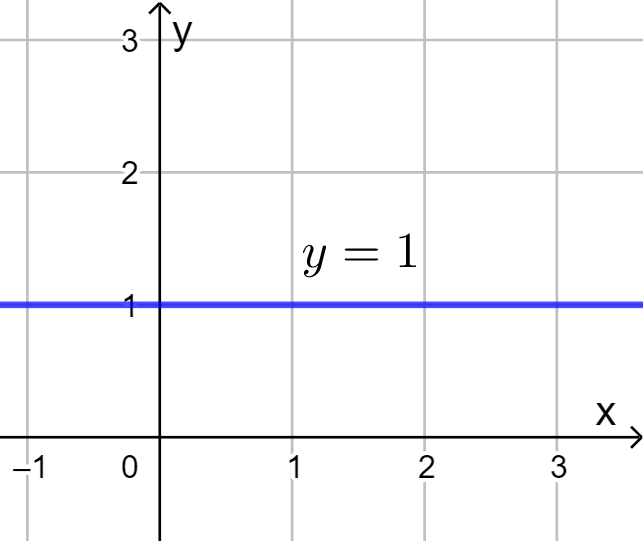
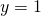 kuvaaja.
kuvaaja.Pistejoukko koostuu pisteistä, joiden ![]() -koordinaatti on
-koordinaatti on ![]() . Olipa
. Olipa ![]() -koordinaatti mikä tahansa,
-koordinaatti mikä tahansa, ![]() -koordinaatti on aina
-koordinaatti on aina ![]() .
.
Piste ![]() ei ole käyrällä, koska
ei ole käyrällä, koska ![]() -koordinaatti ei ole
-koordinaatti ei ole ![]() .
.
Piste ![]() on käyrällä, koska
on käyrällä, koska ![]() -koordinaatti on
-koordinaatti on ![]() .
.
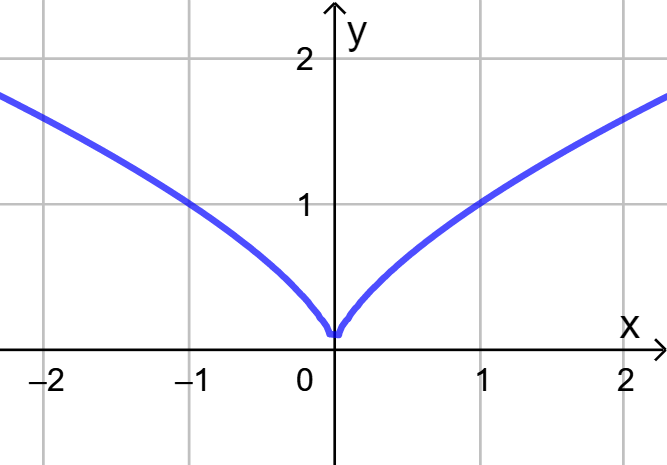
Käyrän yhtälö on ![]() . Piiretään käyrä GeoGebralla.
. Piiretään käyrä GeoGebralla.
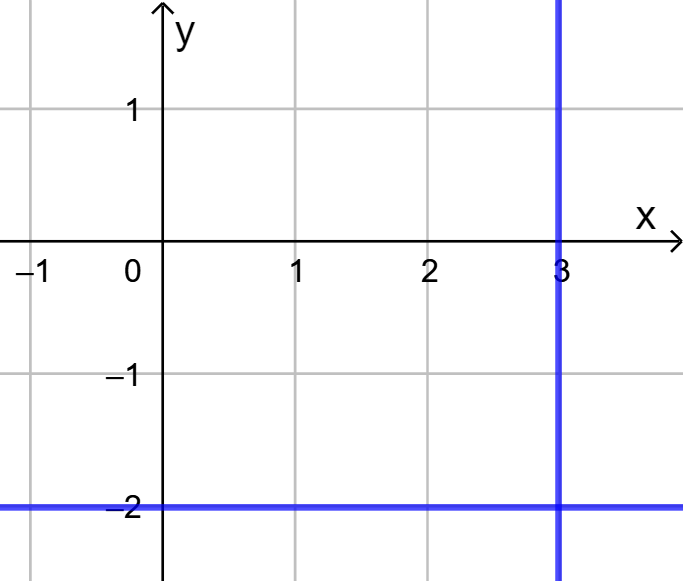
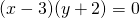
Käyrällä olevat pisteet toteuttavat yhtälön ![]() .
.
Tulon nollasäännön perusteella yhtälö toteutuu, kun jompi kumpi tulon tekijöistä on nolla eli
![]()
tai
![]()
Siten yhtälö ![]() tarkoittaa pistejoukkoa, joka koostuu pisteistä, joiden
tarkoittaa pistejoukkoa, joka koostuu pisteistä, joiden ![]() -koodinaatti on 3
-koodinaatti on 3
ja![]() -koordinaatti on -2.
-koordinaatti on -2.
Kuutio tarkoittaa kolmatta potenssia ja neliö tarkoittaa toista potenssia. Siten käyrän yhtälö on muotoa
![]()
Piirretään käyrä GeoGebralla.
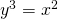
Lasketaan ![]() :n arvot, kun
:n arvot, kun ![]() .
.
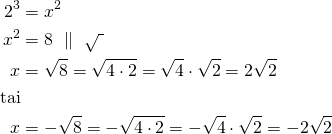
Tämän voisi kirjoittaa myös lyhyemmin seuraavasti:
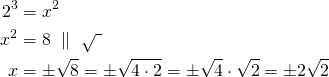
Kysytyt pisteet ovat ![]() ja
ja ![]() .
.
Jos ![]() , niin
, niin ![]() . Tällöin olisi löydettävä sellainen
. Tällöin olisi löydettävä sellainen ![]() -koordinaatti,
-koordinaatti,
että sen neliö on negatiivinen. Tällaisia ei ole, joten yhtälön ![]()
toteuttavien pisteiden joukossa yhdenkään pisteen ![]() -koordinaatti ei ole
-koordinaatti ei ole
negatiivinen.