Tuntimuistiinpanojen ratkaisut
Tuntitehtävien 350, 353, 354, 358 ratkaisut
Määritetään suorien leikkauspiste ratkaisemalla suorista muodostettava yhtälöpari yhteenlaskumenetelmällä:
![Rendered by QuickLaTeX.com \[\begin{cases}2x+3y&=7\\3x-2y&=4\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-af58166eb3af3a72032958a9eeff4eb2_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases}2x+3y&=7\ \parallel\ \cdot 2\\3x-2y&=4\ \parallel\ \cdot 3\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-3e176cc04bfc505ab63b73e833809181_l3.png)
![Rendered by QuickLaTeX.com \[+\begin{cases}4x+6y&=14\\9x-6y&=12\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-c31d1616b967d1ff236609603df89638_l3.png)
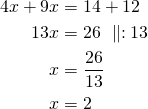
Sijoitetaan jompaan kumpaan suoran yhtälöön saatu ![]() . Käytetään suoran yhtälöä
. Käytetään suoran yhtälöä ![]() .
.
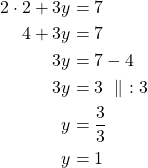
Suorien leikkauspiste on ![]() .
.
Piirretään suorat GeoGebralla.
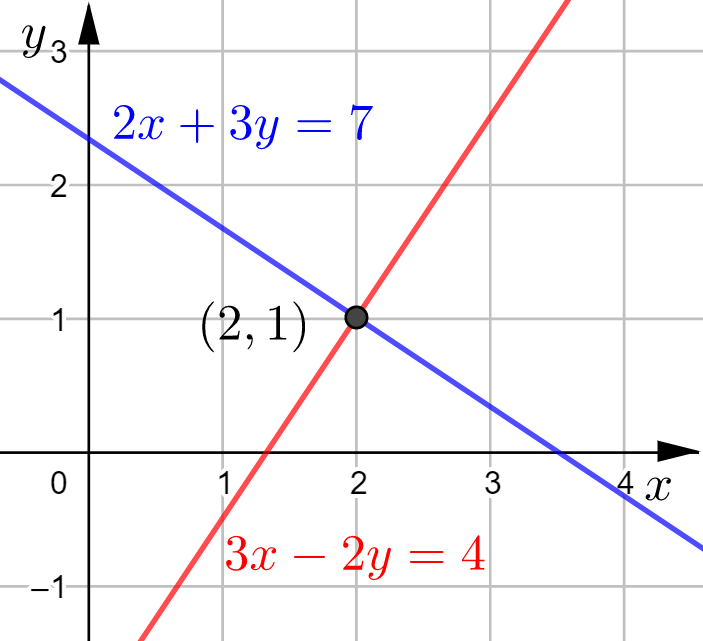
Suorat ovat ![]() ja
ja ![]() .
.
Piirretään suorat GeoGebralla.
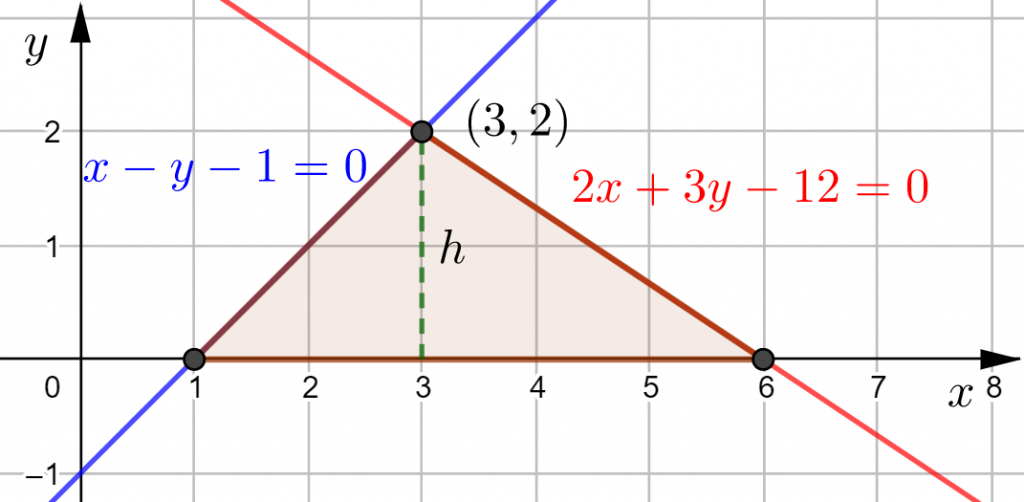
Tällaisessa tehtävässä ei voi katsoa kolmion kärkipisteitä eli suorien leikkauspistettä ja suorien sekä koordinaattiakseleiden leikkauspisteitä kuvasta, vaan ne pitää laskea.
Suorien leikkauspiste:
Ratkaistaan leikkauspiste yhtälöparista
![Rendered by QuickLaTeX.com \[\begin{cases}x-y-1=0\ \parallel\ \cdot 3\\2x+3y-12=0\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-15a27a031c69e0ab917ea6b09875a03b_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases}3x-3y-3=0\\2x+3y-12=0\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-74c433a5539d193e708ee9ef10d4059c_l3.png)
![Rendered by QuickLaTeX.com \[+\begin{cases}3x-3y=3\\2x+3y=12\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-8954b5167091bef89d2c687edd217cad_l3.png)
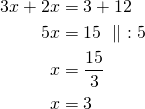
Sijoitetaan ![]() yhtälöön
yhtälöön ![]() ja ratkaistaan
ja ratkaistaan ![]() :
:
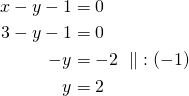
Suorien leikkauspiste on siis ![]() .
.
Suorien ja ![]() -akselin leikkauspisteet
-akselin leikkauspisteet
Kolmion kaksi muuta kärkipistettä ovat ![]() -akselilla.
-akselilla.
Suoran ![]() ja
ja ![]() -akselin leikkauspiste saadaan, kun
-akselin leikkauspiste saadaan, kun ![]() :
:
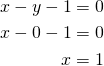
Leikkauspiste on ![]() .
.
Suoran ![]() ja
ja ![]() -akselin leikkauspiste saadaan, kun
-akselin leikkauspiste saadaan, kun ![]() :
:
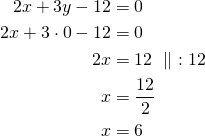
Leikkauspiste on ![]() .
.
Kolmion kanta on pisteiden ![]() ja
ja ![]() etäisyys, eli
etäisyys, eli ![]() .
.
Kolmion korkeus ![]() saadaan suorien leikkauspisteen
saadaan suorien leikkauspisteen ![]() -koordinaatista,
-koordinaatista,
joka on ![]() .
.
Kolmion pinta-ala on
![]()
Vastaus: Kolmion pinta-ala on ![]() .
.
Piirretään GeoGebralla suorat ![]() ja
ja ![]() .
.
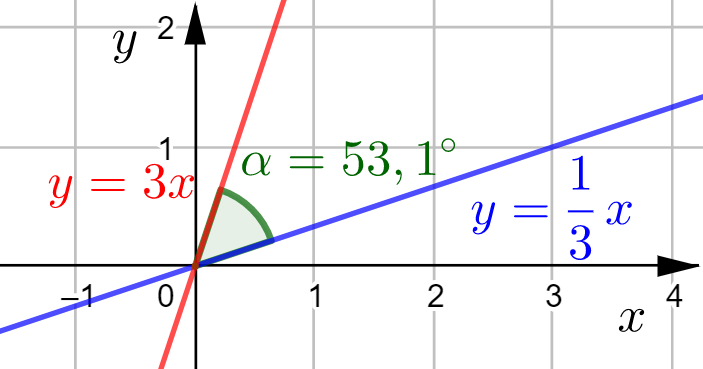
Suorien välisen kulman suuruus on ![]() .
.
Suorien välilen kulma voidaan laskea kaavalla
![]()
Sijoitetaan kaavaan ![]() ja
ja ![]()
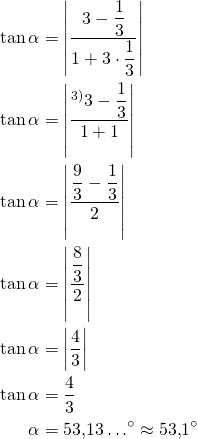
Vastaus: Suorien välinen kulma on ![]() .
.
Selvitetään ensin suorien ![]() ja
ja ![]() kulmakertoimet suorien yhtälöiden ratkaistuista muodoista.
kulmakertoimet suorien yhtälöiden ratkaistuista muodoista.
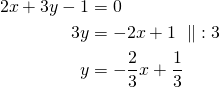
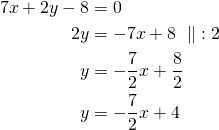
Sijoitetaan suorien kulmakertoimet ![]() ja
ja ![]() lausekkeeseen
lausekkeeseen
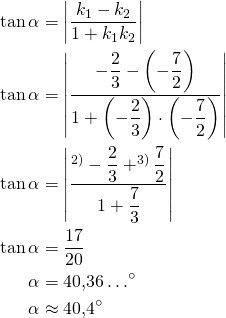
Suora ![]() on pystysuora, joten kysytty kulma saadaan laskettua
on pystysuora, joten kysytty kulma saadaan laskettua
suoran kulman ja suoran ![]() suuntakulman erotuksena.
suuntakulman erotuksena.
Suoran ![]() , eli suoran
, eli suoran ![]() kulmakerroin on
kulmakerroin on ![]() .
.
![]()
Siten suorien ![]() ja
ja ![]() välinen kulma on
välinen kulma on![]() .
.
Kotitehtävien 351, 355, 361, 367 ratkaisut
A Ratkaistaan yhtälöpari sijoitusmenetelmällä siten, että sijoitetaan alemmasta yhtälöstä ratkaistu ![]() :n lauseke ylempään yhtälöön
:n lauseke ylempään yhtälöön ![]() :n paikalle.
:n paikalle.
![Rendered by QuickLaTeX.com \[\begin{cases}2x-3y=2\\y=\dfrac{2}{3}x+\dfrac{1}{3}\\\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-d666aa28e711c4957634bcb52a1693f0_l3.png)
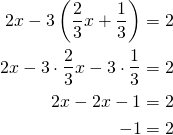
Yhtälöparilla ei ole ratkaisua, mikä tarkoittaa sitä, että suorat ovat yhdensuuntaiset.
Kuva III liittyy tähän.
B Ratkaistaan yhtälöpari sijoitusmenetelmällä.
![Rendered by QuickLaTeX.com \[\begin{cases}x+3y=7\\y=x-1\\\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-5405dabdbedf3b9c28ae3545ec8ec7bd_l3.png)
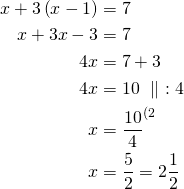
Sijoitetaan saatu ![]() :n arvo yhtälöön
:n arvo yhtälöön ![]() , jolloin
, jolloin![]()
Yhtälöparin ratkaisu on ![]() .
.
Kuva I liittyy tähän.
C Ratkaistaan yhtälöpari sijoitusmenetelmällä.
![Rendered by QuickLaTeX.com \[\begin{cases}y=-2x+5\\2x+y=5\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-813bc4187d9dc1390fdb4af2b780d9ad_l3.png)
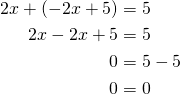
Tämä tarkoittaa sitä, että yhtälöpari toteutuu kaikilla muuttujan ![]() arvoilla. Siis ratkaisuna ovat kaikki suoran
arvoilla. Siis ratkaisuna ovat kaikki suoran ![]() pisteet. Yhtälöparin suorat ovat siis sama suora.
pisteet. Yhtälöparin suorat ovat siis sama suora.
Kuva II liittyy tähän.
Huom! Jos muokataan yhtälöparin ylempää yhtälöä muotoo ![]() , huomataan, että kyseessä ovat samat yhtälöt.
, huomataan, että kyseessä ovat samat yhtälöt.
![Rendered by QuickLaTeX.com \[\begin{cases}2x+y=5\\2x+y=5\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-f539b2080df0d72d33049d6ea0b38fef_l3.png)
Ratkaistaan suorien leikkauspisten yhtälöparilla.
![Rendered by QuickLaTeX.com \[\begin{cases}\dfrac{x}{3}+\dfrac{y}{2}=1\ \parallel\ \cdot 6\\3x-2y+3=0\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-70026bf5f41bf8df03db9c75ad32ce3a_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases}6 \cdot \dfrac{x}{3}+6 \cdot \dfrac{y}{2}=6 \cdot 1\\3x-2y=-3\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-17f7b63189abd2130fa8acf887f72539_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases}2x+3y=6\ \parallel\ \cdot 3\\3x-2y=-3\ \parallel\ \cdot (-2)\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-bb47168d26be6982497fec86d84401a7_l3.png)
![Rendered by QuickLaTeX.com \[+\begin{cases}6x+9y=18\ \parallel\\-6x+4y=6\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-0388ebb3612650d0fed68f36dbd0ed2c_l3.png)
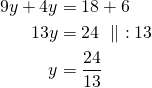
Ratkaistaan ![]() sijoittamalla
sijoittamalla ![]() yhtälöön
yhtälöön ![]() .
.
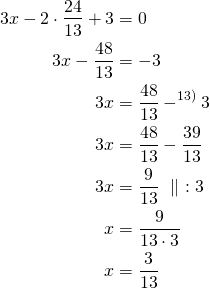
Suorien leikkauspiste on ![]() .
.
Muodostetaan käyrän yhtälö.
![]()
Tehtävän idea: On osoitettava, että käyrä muodostuu kahdesta yhdensuuntaisesta suorasta eli suorista, joilla on sama kulmakerroin.
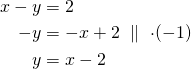
tai
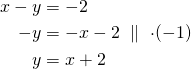
Kummankin suoran kulmakerroin on ![]() , joten pistejoukko
, joten pistejoukko ![]() koostuu kahdesta yhdensuuntaisesta suorasta
koostuu kahdesta yhdensuuntaisesta suorasta ![]() ja
ja ![]() .
.
Suorien yhtälöt ovat ![]() ja
ja ![]() . Kummatkin suorat kulkevat pisteen
. Kummatkin suorat kulkevat pisteen ![]() kautta.
kautta.
Sijoitetaan pisteen ![]() koordinaatit suorien yhtälöihin.
koordinaatit suorien yhtälöihin.
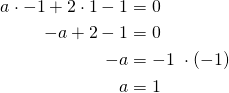
Sekä
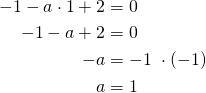
Kun ![]() , molemmat suorat kulkevat pisteen
, molemmat suorat kulkevat pisteen ![]() kautta.
kautta.