Tehtävät 521, 522, 523, 530
A-II, B-II ja III, C-I ja II, D-III
Pisteen ![]() etäisyys johtosuorasta
etäisyys johtosuorasta ![]() on
on ![]() .
.
Pisteen ![]() etäisyys polttopisteestä
etäisyys polttopisteestä ![]() on
on![]() -koordinaattien erotus
-koordinaattien erotus ![]() .
.
Toisenkin pisteen ![]() -koordinaatti pitää olla
-koordinaatti pitää olla ![]() , jotta etäisyys johtosuorasta pysyy samana. Piste
, jotta etäisyys johtosuorasta pysyy samana. Piste ![]() sijaitsee symmetrisesti polttopisteen toisella puolella pisteeseen
sijaitsee symmetrisesti polttopisteen toisella puolella pisteeseen ![]() nähden.
nähden.
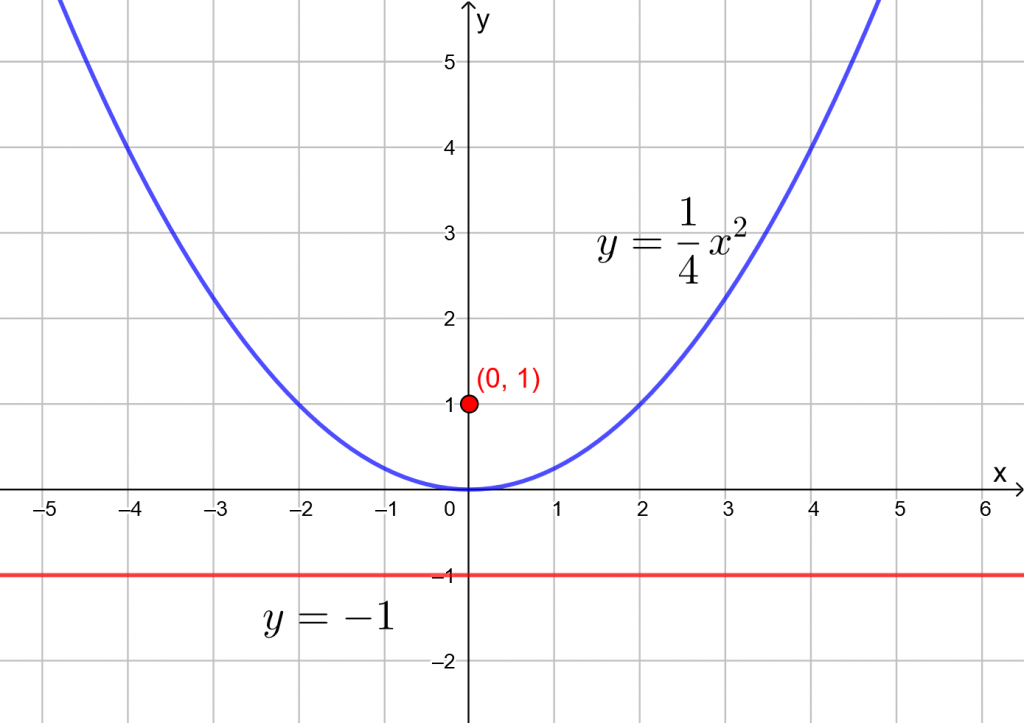
Merkitään paraabelin yleistä pistettä ![]() . Lasketaan sen etäisyys polttopisteestä
. Lasketaan sen etäisyys polttopisteestä ![]() sekä johtosuorasta
sekä johtosuorasta ![]() ja merkitään lasketut etäisyydet yhtäsuuriksi.
ja merkitään lasketut etäisyydet yhtäsuuriksi.
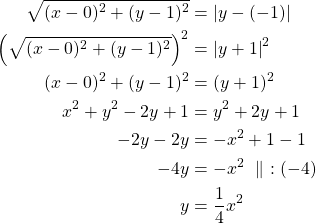
Vastaus: Paraabelin yhtälö on ![]() .
.
Videolla esitetään paraabelin määrittäminen annettujen pisteiden avulla GeoGebran SovitaPolynomi-komennolla.
Video tehtävästä 530.
Kotitehtävät 527, 528 ja 535.
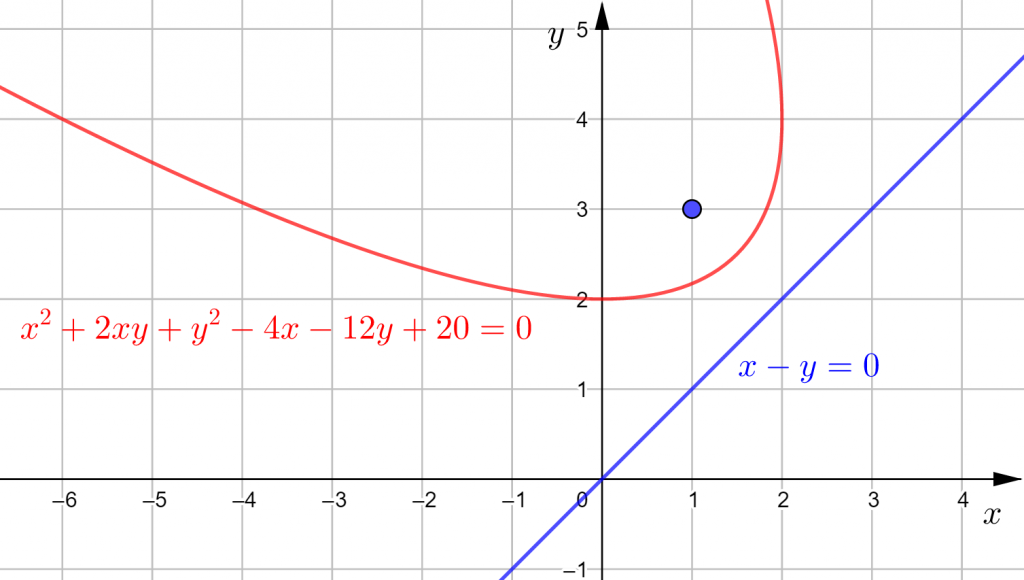
Paraabeli aukeaa joko vasemmalle tai oikealle, koska paraabelin johtosuora on ![]() -akselin suuntainen.
-akselin suuntainen.
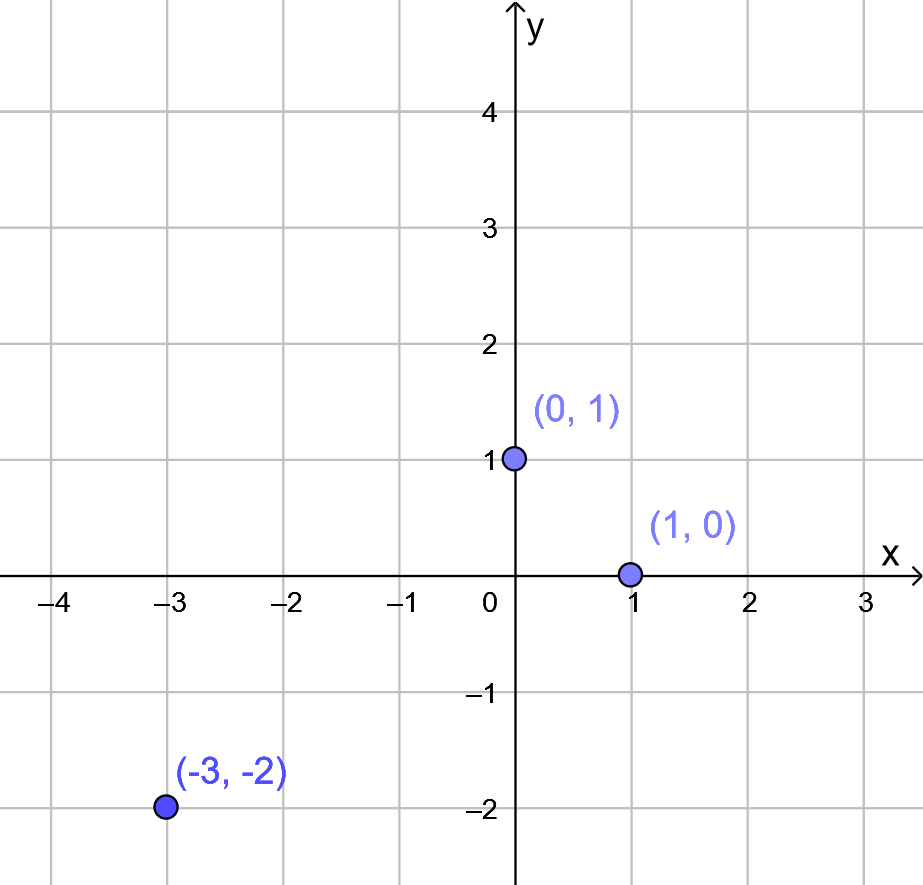
Koordinaatistoon piirrettyjen pisteiden perusteella aukeamisuunan voidaan päätellä olevan vasemmalle, koska piste ![]() on oikean puoleisin ja korkeimmalla.
on oikean puoleisin ja korkeimmalla.
Koska paraabeli on vasemmalle aukeava, sen yhtälä on muotoa ![]() . Sijoitetaan pisteet
. Sijoitetaan pisteet ![]() ,
, ![]() ja
ja ![]() tähän yhtälöön.
tähän yhtälöön.
![]() , mistä saadaan
, mistä saadaan ![]()
![]() , mistä saadaan
, mistä saadaan ![]()
![]() , mistä saadaan
, mistä saadaan ![]()
Muodosteaan yhtälöryhmä
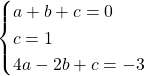
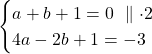
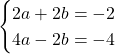
![]()
Kun ![]() ja
ja ![]() , niin
, niin ![]() , josta
, josta ![]() .
.
Paraabelin yhtälö on ![]() .
.
Paraabelin yhtälö on muotoa ![]() , koska sen johtosuora on
, koska sen johtosuora on ![]() -akselin suuntainen.
-akselin suuntainen.
Sijoitetaan pisteet ![]() ,
, ![]() ja
ja ![]() paraabelin yhtälöön.
paraabelin yhtälöön.
Piste ![]()
![]()
Tästä saadaan ![]() eli
eli ![]() .
.
Piste ![]()
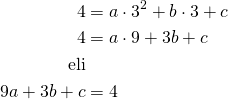
Piste ![]()
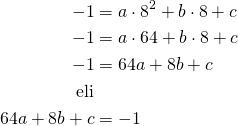
Tehdään näistä kolmesta htälöstä yhtälöryhmä.
![Rendered by QuickLaTeX.com \[\begin{cases}c=1\\9a+3b+c=4\\64a+8b+c=-1\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-5eee8e779ab166483479e034d8187f9f_l3.png)
Ratkaistaan kertoimet ![]() ,
, ![]() ja
ja ![]() GeoGebralla. Ratkaisu on
GeoGebralla. Ratkaisu on
![Rendered by QuickLaTeX.com \[\begin{cases}a=-\frac{1}{4}\\b=\frac{7}{4}\\c=1\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-a101e752c0c26faf5bfca662be689a2b_l3.png)
Vastaus: Paraabelin yhtälö on ![]() .
.
Paraabelin yhtälö on muotoa ![]() , koska sen johtosuora on
, koska sen johtosuora on ![]() -akselin suuntainen.
-akselin suuntainen.
Sijoitetaan pisteet ![]() ,
, ![]() ja
ja ![]() paraabelin yhtälöön.
paraabelin yhtälöön.
Piste ![]()
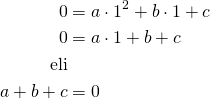
Piste ![]()
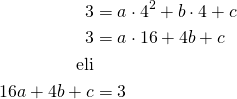
Piste ![]()
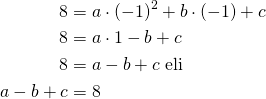
Tehdään näistä kolmesta yhtälöstä yhtälöryhmä.
![Rendered by QuickLaTeX.com \[\begin{cases}a+b+c=0\\16a+4b+c=3\\a-b+c=8\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-9acd3911084a3eff28dd48f73e46fc62_l3.png)
Ratkaistaan kertoimet ![]() ,
, ![]() ja
ja ![]() GeoGebralla. Ratkaisu on
GeoGebralla. Ratkaisu on
![Rendered by QuickLaTeX.com \[\begin{cases}a=1\\b=-4\\c=3\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-0a67f9eb5fcd6e9510dcbfca118fe2f7_l3.png)
Vastaus: Paraabelin yhtälö on ![]() .
.
Merkitään pistettä ![]() kysytyllä paraabelilla. Lasketaan sen etäisyys polttopisteestä
kysytyllä paraabelilla. Lasketaan sen etäisyys polttopisteestä ![]() ja johtosuorasta
ja johtosuorasta ![]() . Etäisyydet ovat yhtä suuret, joten saadaan yhtälö
. Etäisyydet ovat yhtä suuret, joten saadaan yhtälö
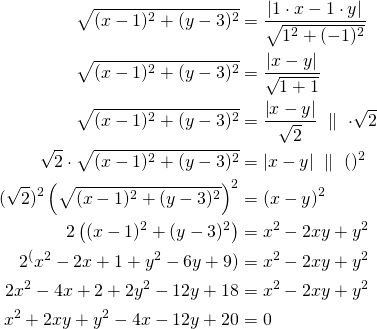
Piirretään kuva GeoGebralla.