Tuntitehtävät 501, 502, 503, 504, 511
A-IV. Perustelu
- Toisen asteen termissä on muuttujana
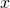 , joten paraabelin akseli on
, joten paraabelin akseli on 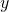 -akselin suuntainen.
-akselin suuntainen. - Sen kerroin
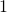 on positiivinen, joten aukeamissuunta on ylöspäin.
on positiivinen, joten aukeamissuunta on ylöspäin.
B-I. Perustelu
- Toisen asteen termissä on muuttujana
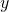 , joten paraabelin akseli on
, joten paraabelin akseli on 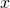 -akselin suuntainen.
-akselin suuntainen. - Sen kerroin
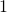 on positiivinen, joten aukeamissuunta on oikealle.
on positiivinen, joten aukeamissuunta on oikealle.
C-II. Perustelu
- Toisen asteen termissä on muuttujana
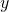 , joten paraabelin akseli on
, joten paraabelin akseli on 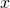 -akselin suuntainen.
-akselin suuntainen. - Sen kerroin
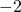 on negatiivinen, joten aukamissuunta on vasemmalle.
on negatiivinen, joten aukamissuunta on vasemmalle.
D-III. Perustelu
- Toisen asteen termissä on muuttujana
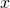 , joten paraabelin akseli on
, joten paraabelin akseli on 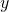 -akselin suuntainen.
-akselin suuntainen. - Sen kerroin
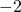 on positiivinen, joten aukeamissuunta on alaspäin.
on positiivinen, joten aukeamissuunta on alaspäin.
- Toisen asteen termissä
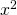 on muuttujana
on muuttujana 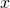 , joten paraabelin akseli on
, joten paraabelin akseli on 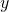 -akselin suuntainen.
-akselin suuntainen. - Sen kerroin
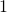 on positiivinen, joten aukamissuunta on ylöspäin.
on positiivinen, joten aukamissuunta on ylöspäin. - Paraabelin akseli on suora
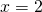 , koska paraabeli on ylöspäin aukeava ja huipun
, koska paraabeli on ylöspäin aukeava ja huipun 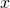 -koordinaatti on
-koordinaatti on 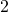 .
.
- Toisen asteen termissä
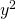 on muuttujana
on muuttujana 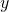 , joten paraabelin akseli on
, joten paraabelin akseli on 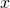 -akselin suuntainen.
-akselin suuntainen. - Sen kerroin
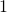 on positiivinen, joten aukamissuunta on oikealle.
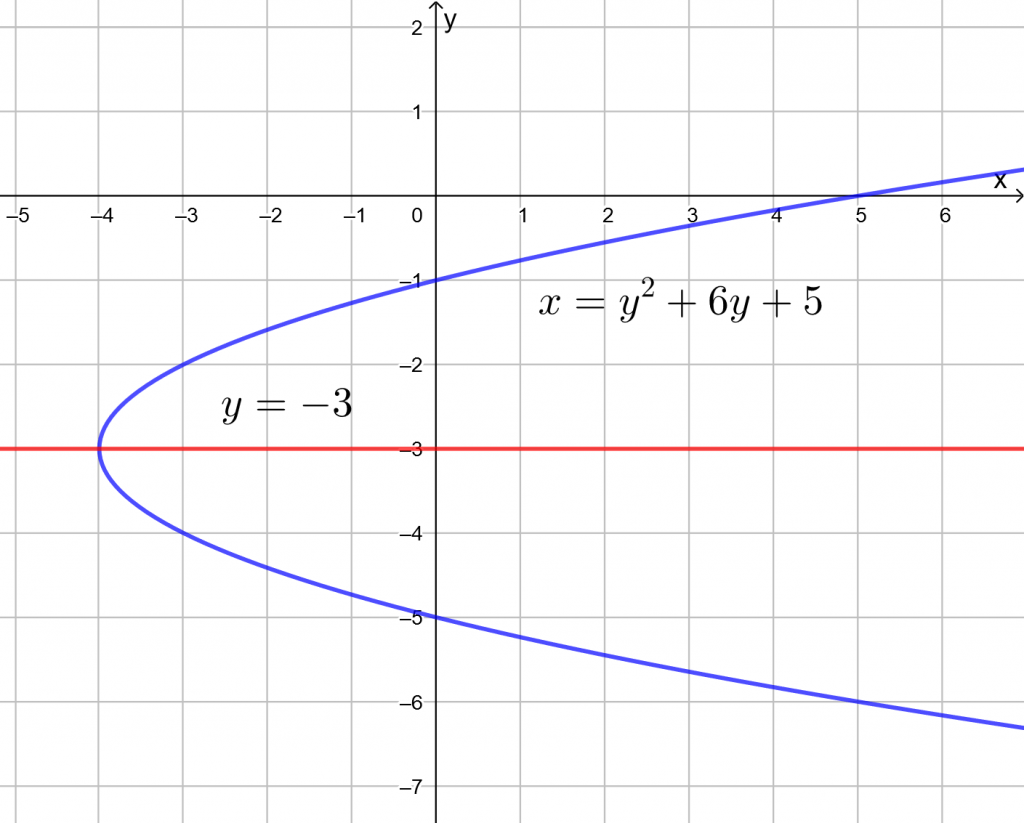
on positiivinen, joten aukamissuunta on oikealle. - Paraabelin akseli on suora
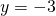 , koska paraabeli on ylöspäin aukeava ja huipun
, koska paraabeli on ylöspäin aukeava ja huipun 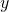 -koordinaatti on
-koordinaatti on 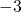 .
.
- Toisen asteen termissä
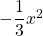 on muuttujana
on muuttujana 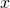 , joten paraabelin akseli on
, joten paraabelin akseli on 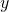 -akselin suuntainen.
-akselin suuntainen. - Sen kerroin
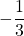 on negatiivinen, joten aukamissuunta on alaspäin.
on negatiivinen, joten aukamissuunta on alaspäin. - Paraabelin akseli on suora
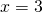 , koska paraabeli on alaspäin aukeava ja huipun
, koska paraabeli on alaspäin aukeava ja huipun 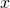 -koordinaatti on
-koordinaatti on 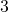 .
.
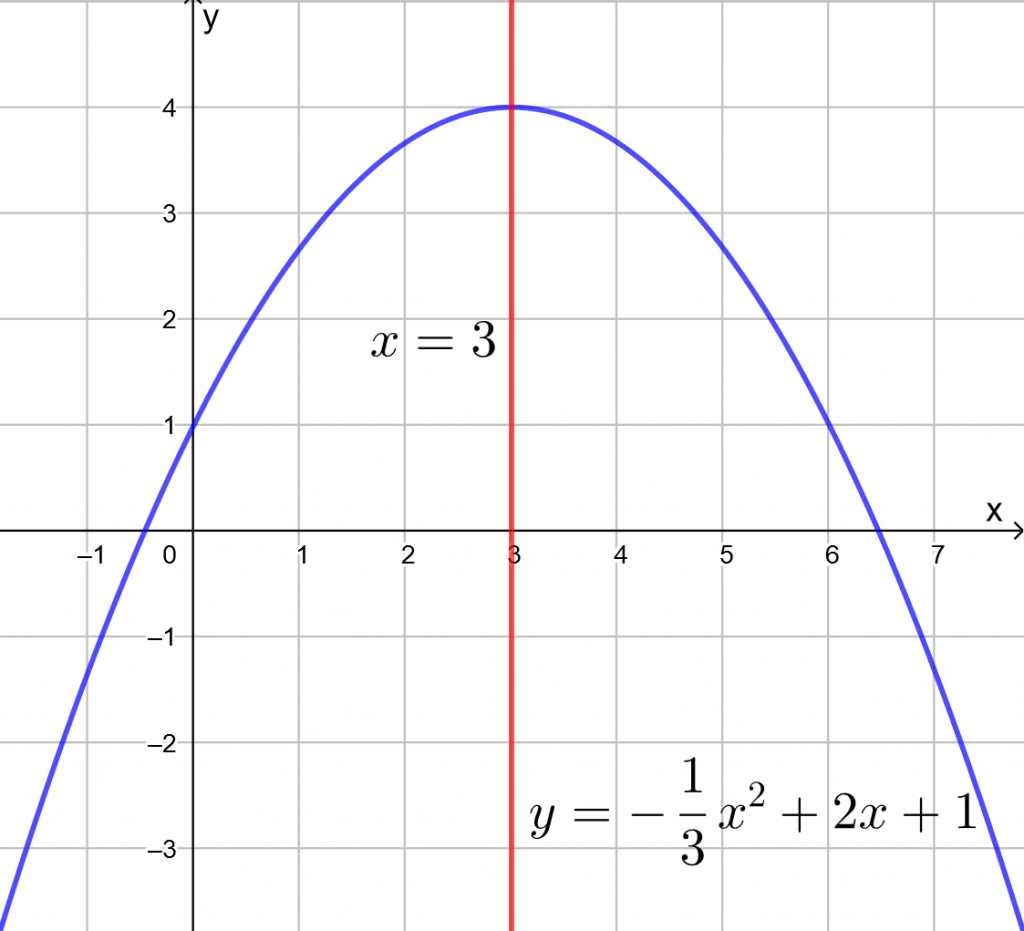
- Toisen asteen termissä
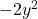 on muuttujana
on muuttujana 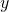 , joten paraabelin akseli on
, joten paraabelin akseli on 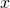 -akselin suuntainen.
-akselin suuntainen. - Sen kerroin
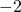 on negatiivinen, joten aukamissuunta on vasemmalle.
on negatiivinen, joten aukamissuunta on vasemmalle. - Paraabelin akseli on suora
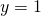 , koska paraabeli on vasemmalle aukeava ja huipun
, koska paraabeli on vasemmalle aukeava ja huipun 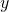 -koordinaatti on
-koordinaatti on 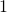 .
.
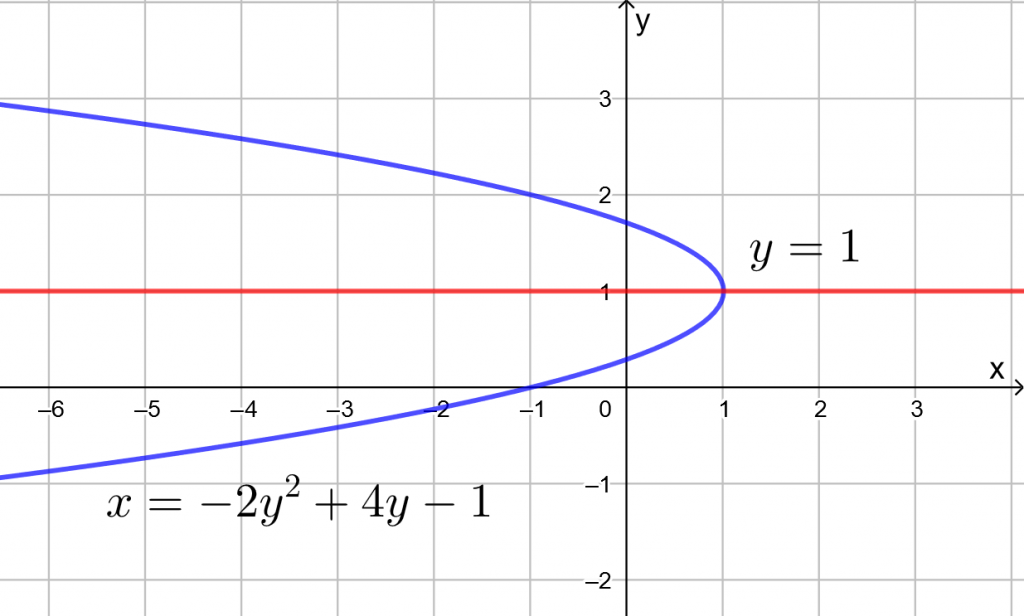
Paraabelin ![]() ja
ja ![]() -akselin leikkauspisteissä
-akselin leikkauspisteissä ![]() -koordinaatti on nolla.
-koordinaatti on nolla.
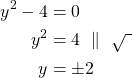
Leikkauspisteet ovat ![]() ja
ja ![]() .
.
Paraabelin huipun ![]() -koordinaatti on
-koordinaatti on ![]() -akselin leikkauskohtien puolivälissä:
-akselin leikkauskohtien puolivälissä:
![]() .
.
Huipun ![]() -koordinaatti on
-koordinaatti on ![]() .
.
Huippu on pisteessä ![]() .
.
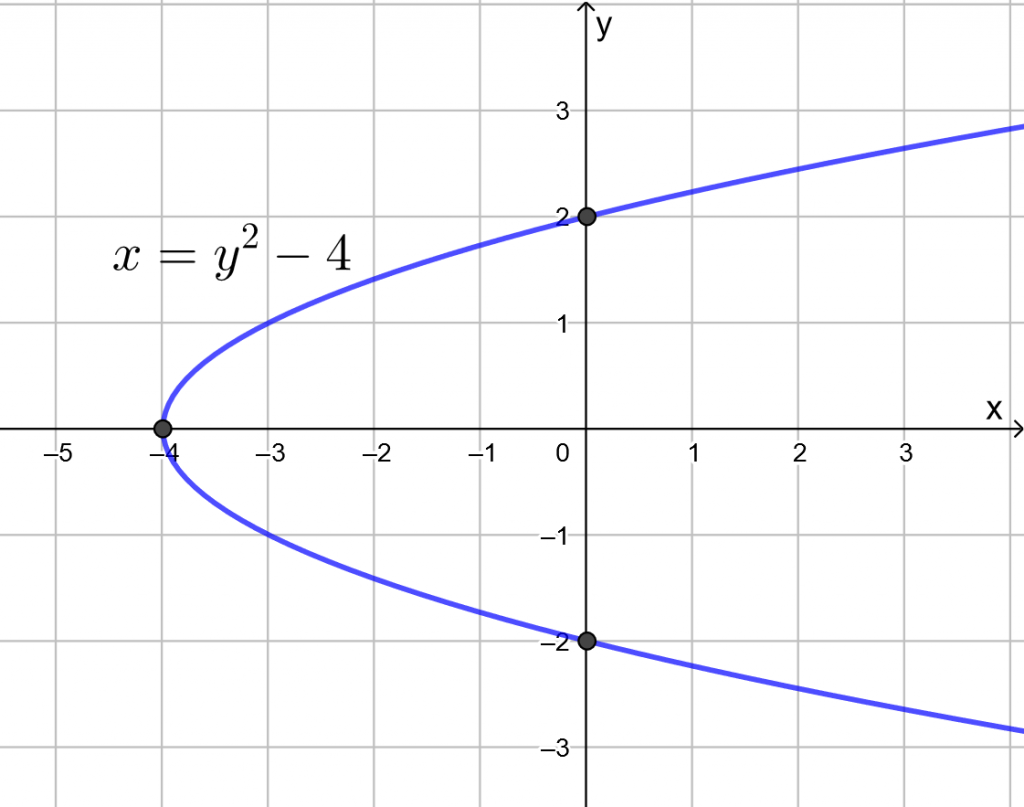
Hahmotellaan paraabeli yllä laskettujen pisteiden avulla koordinaatistoon. Paraabeli aukeamissuunta on oikealle, koska toisen asteen termin ![]() kerroin
kerroin ![]() on positiivinen.
on positiivinen.
Paraabelin ![]() ja
ja ![]() -akselin leikkauspisteissä
-akselin leikkauspisteissä ![]() -koordinaatti on nolla.
-koordinaatti on nolla.
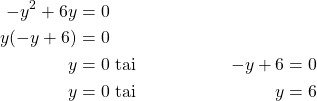
Leikkauspisteet ovat ![]() ja
ja ![]() .
.
Paraabelin huipun ![]() -koordinaatti on
-koordinaatti on ![]() -akselin leikkauskohtien puolivälissä:
-akselin leikkauskohtien puolivälissä:
![]() .
.
Huipun ![]() -koordinaatti on
-koordinaatti on ![]() .
.
Huippu on pisteessä ![]() .
.
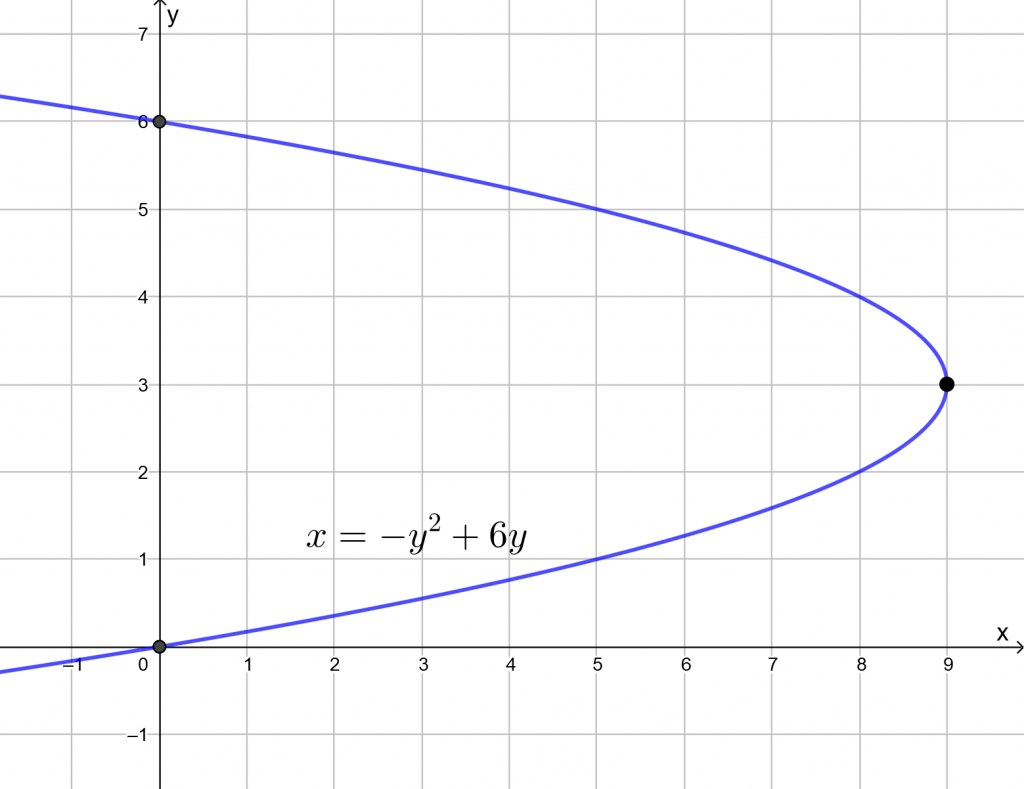
Hahmotellaan paraabeli yllä laskettujen pisteiden avulla koordinaatistoon. Paraabeli aukeamissuunta on vasemmalle, koska toisen asteen termin ![]() kerroin
kerroin ![]() on negatiivinen.
on negatiivinen.
Käyrä ![]() voidaan kirjoittaa muodossa
voidaan kirjoittaa muodossa ![]() .
.
Kysessä on vasemmalle aukeava paraabeli, jonka leikkauspisteissä ![]() -akselin kanssa
-akselin kanssa ![]() -koordinaatti on nolla.
-koordinaatti on nolla.
![]() .
.
Leikkauspiste on ![]() .
.
Käyrän ja ![]() -akselin leikkauspisteissä
-akselin leikkauspisteissä ![]() -koordinaatti on nolla.
-koordinaatti on nolla.
![]()
Kysessä on toisen asteen yhtälö. Ratkaistaan se, kun
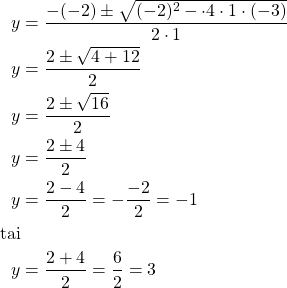
Leikkauspisteet ovat siten ![]() ja
ja ![]() .
.
Paraabelin huipun ![]() -koordinaatti on
-koordinaatti on ![]() -akselin leikkauskohtien puolivälissä:
-akselin leikkauskohtien puolivälissä:
![]() .
.
Huipun ![]() -koordinaatti on
-koordinaatti on ![]() .
.
Huippu on pisteessä ![]() .
.
Hahmotellaan paraabelin kuvaaja yllä olevien tietojen perusteella.
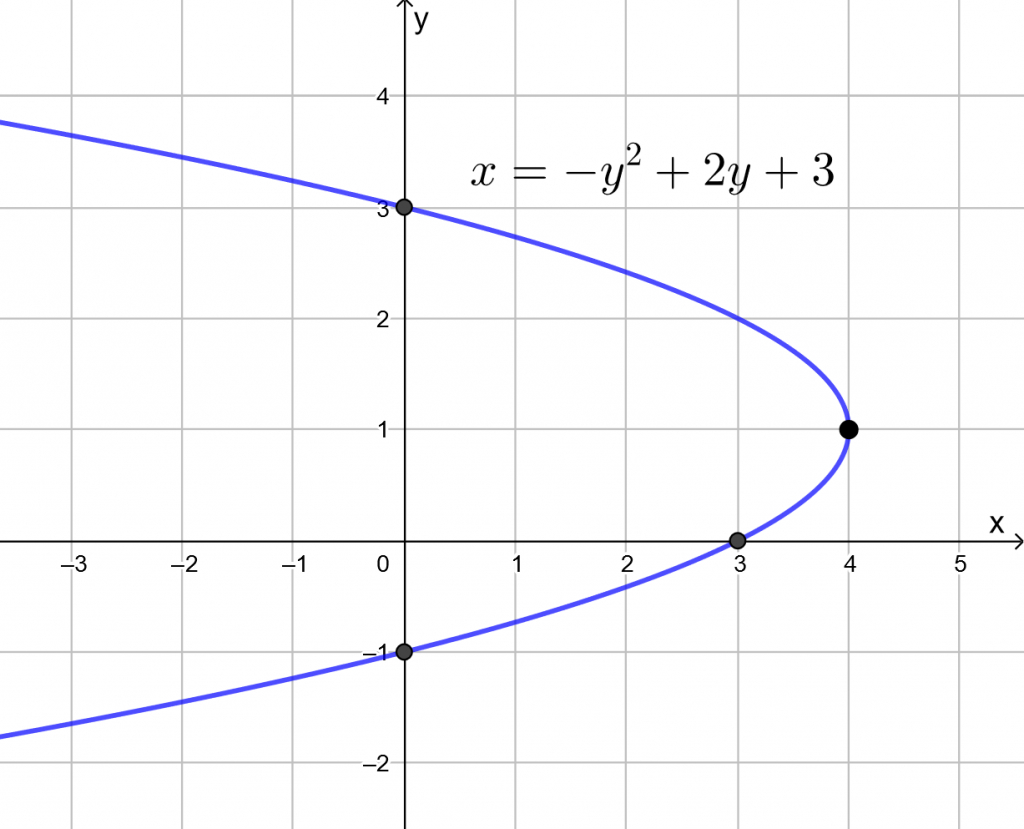
Paraabeli aukeaa oikealle, joten paraabelin yhtälö on muotoa
![]() , missä
, missä ![]() .
.
Sijoitetaan yhtälöön huipun ![]() koordinaatit.
koordinaatit.
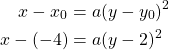
Paraabeli kulkee origon eli pisteen ![]() kautta, joten piste
kautta, joten piste ![]() toteuttaa paraabelin yhtälön.
toteuttaa paraabelin yhtälön.
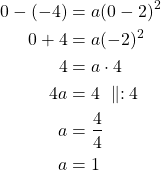
SIjoitetaan paraabelin yhtälöön ![]() ja
ja ![]() , jolloin saadaan
, jolloin saadaan
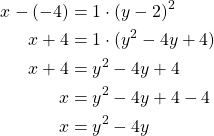
Kotitehtävät 505, 506, 507, 513, 514, 515, 518
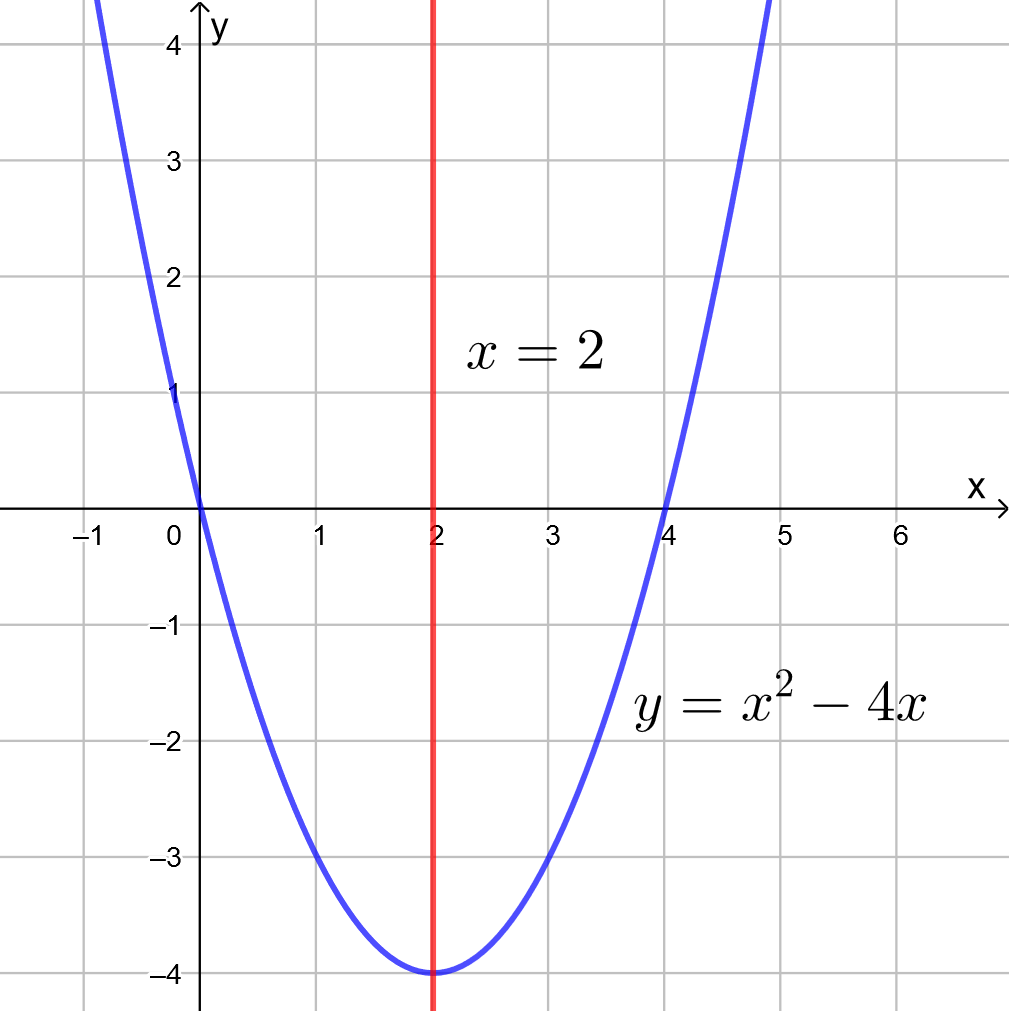
Ratkaistaan suoran ja paraabelin leikkauspisteet. Ne saadaan yhtälöparista
![Rendered by QuickLaTeX.com \[\begin{cases}x+y=2\\y=x^2-4x+2\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-cb3c5235d7882d866ce313d3cfb4b0cd_l3.png)
Ratkaistaan suoran yhtälöstä ![]() ja sijoitetaan se paraabelin yhtälöön.
ja sijoitetaan se paraabelin yhtälöön.
![Rendered by QuickLaTeX.com \[\begin{cases}y=2-x\\y=x^2-4x+2\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-18f9cf0edf3c80a65b12d18774748cf9_l3.png)
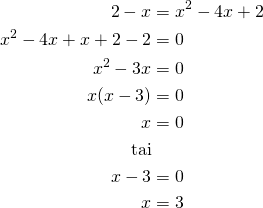
Ratkaistaan ![]() :n arvot.
:n arvot.
Kun ![]() , niin
, niin ![]() . Leikkauspiste on
. Leikkauspiste on ![]() .
.
Kun ![]() , niin
, niin ![]() . Leikkauspiste on
. Leikkauspiste on ![]() .
.
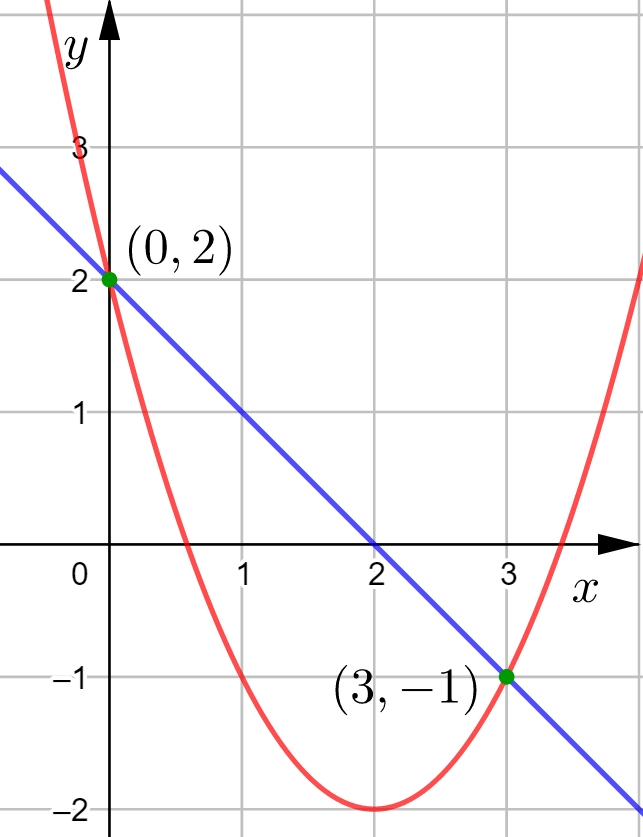
Piirretään kuva GeoGebralla.
Lasketaan paraabelien ![]() ja
ja ![]() leikkauspisteet yhälöparista sijoitusmenetelmällä.
leikkauspisteet yhälöparista sijoitusmenetelmällä.
![Rendered by QuickLaTeX.com \[\begin{cases}y=x^2\\x=y^2\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-869701c13354cdf758a362c802d39206_l3.png)
Sijoitetaan alempaan yhtälöön ![]() :n paikalle
:n paikalle ![]() . Tällöin
. Tällöin
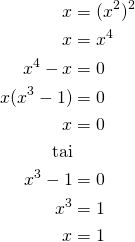
Lasketaan ![]() :n arvot, kun
:n arvot, kun![]() , niin
, niin ![]()
ja![]() , niin
, niin ![]()
Leikkauspisteet ovat ![]() ja
ja ![]() .
.
Piirretään kuva GeoGebralla.
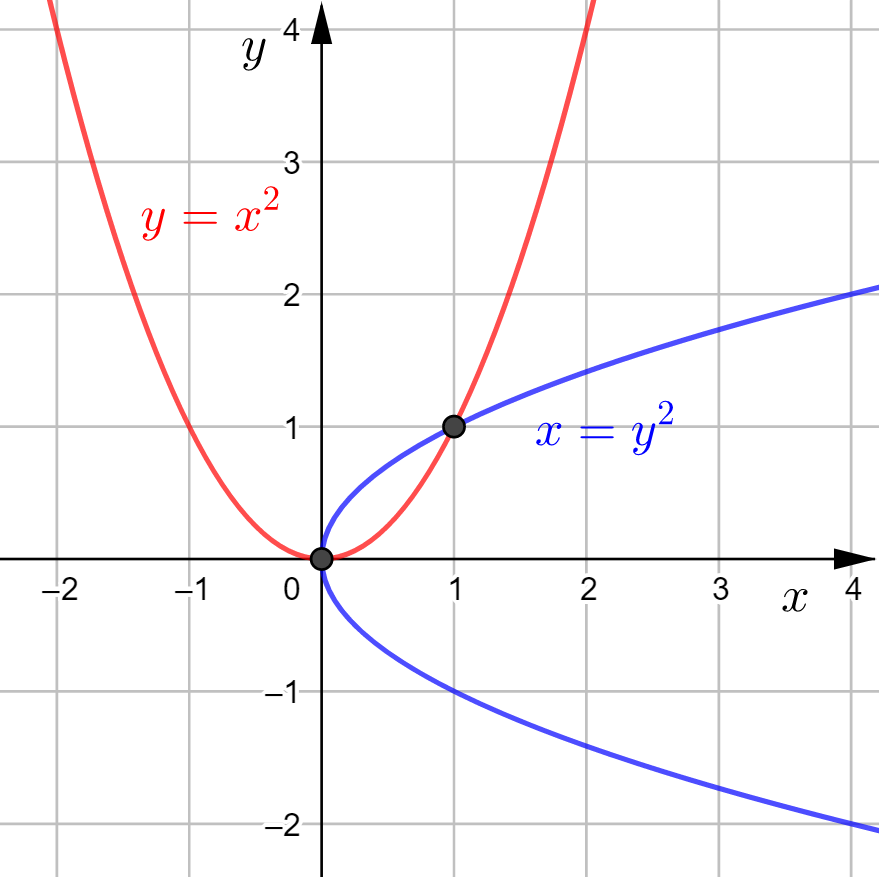
Paraabelin ![]() ja ympyrän
ja ympyrän ![]() leikkauspisteet saadaan ratkaistua yhtälöparista
leikkauspisteet saadaan ratkaistua yhtälöparista
![Rendered by QuickLaTeX.com \[\begin{cases}x-2y^2+1=0\ \ \text{ratkaistaan}\ x=2y^2-1\\x^2+y^2=2\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-fca9bf79e757d59af8ed4d2ed5ad92eb_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases}x=2y^2-1\\x^2+y^2=2\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-a4f5e919a6a32f37cb8b63993e55c559_l3.png)
Sijoitetaan alempaan yhtälöön ![]() :n paikalle
:n paikalle ![]()
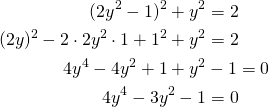
Tästä voidaan ratkaista ![]() , kun sijoitetaan
, kun sijoitetaan ![]() :n tilalle lauseke
:n tilalle lauseke ![]() . Yhtälö muuttuu toisen asteen yhtälöksi.
. Yhtälö muuttuu toisen asteen yhtälöksi.
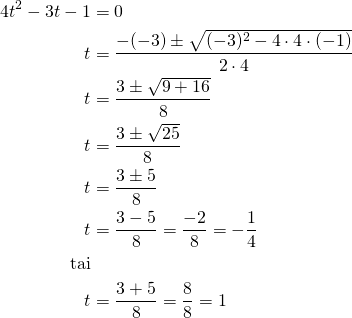
Ratkaistaan nyt ![]() .
.
Kun ![]() , saadaan
, saadaan
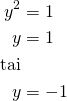
Kun ![]() , saadaan
, saadaan
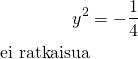
Ratkaistaan sitten ![]() :n arvot.
:n arvot.
Kun ![]() ,
, ![]() .
.
Kun ![]() ,
, ![]() .
.
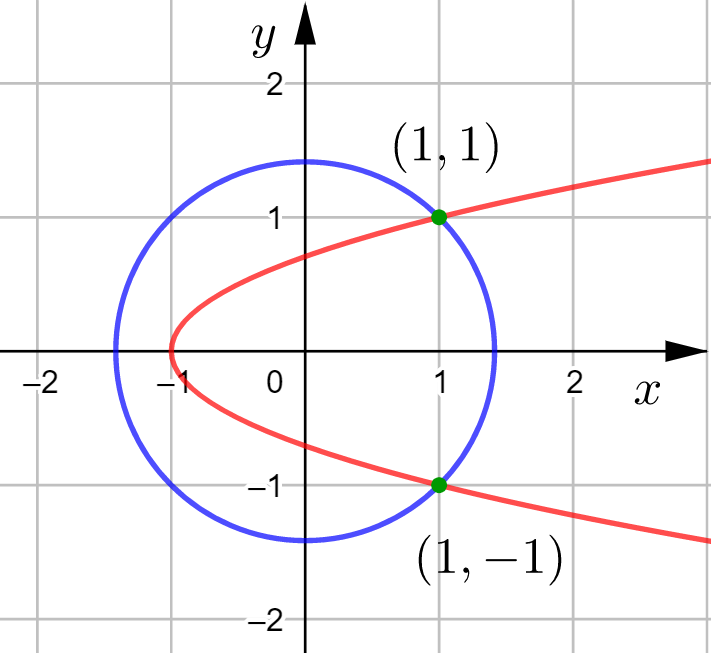
Leikkauspisteet ovat ![]() ja
ja ![]() .
.
Tarkistetaan GeoGebralla.
Ylöspäin avautuvan paraabelin huippu on pisteessä ![]() ja se kulkee pisteen
ja se kulkee pisteen ![]() kautta.
kautta.
Ylöspäin avautuvan paraabelin yhtälö on muotoa ![]() .
.
Sijoitetaan yhtälöön huipun ![]() koordinaatit.
koordinaatit.
![]()
Koska paraabeli kulkee pisteen ![]() kautta, piste toteuttaa paraabelin yhtälön.
kautta, piste toteuttaa paraabelin yhtälön.
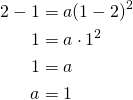
Paraabelin yhtälö on
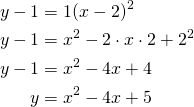
Sijoitetaan pisteiden ![]() ,
, ![]() ja
ja ![]() koordinaatit paraabelin yhtälöön.
koordinaatit paraabelin yhtälöön.
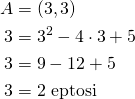
Piste ![]() ei ole paraabelilla.
ei ole paraabelilla.
Kun ![]() ja
ja ![]() , eli paraabelilla on piste
, eli paraabelilla on piste ![]() . Siten piste
. Siten piste ![]() on paraabelin yläpuolella.
on paraabelin yläpuolella.
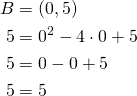
Piste ![]() on paraabelilla.
on paraabelilla.
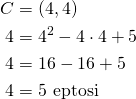
Kun ![]() ja
ja ![]() , eli paraabelilla on piste
, eli paraabelilla on piste ![]() . Siten piste
. Siten piste ![]() on paraabelin alapuolella.
on paraabelin alapuolella.
Pisteet, jotka ovat etäisyydellä ![]() pisteestä
pisteestä ![]() ovat ympyrällä
ovat ympyrällä ![]() . Selvitetään paraabelin
. Selvitetään paraabelin ![]() ja ympyrän leikkauspisteet.
ja ympyrän leikkauspisteet.
![Rendered by QuickLaTeX.com \[\begin{cases}x=-y^2+3\ \ \text{ratkaistaan}\ y^2=-x+3\\(x+2)^2+y^2=25\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-54b902bdc9afc9b0cb414474e24ca374_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} y^2=-x+3\\(x+2)^2+y^2=25\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-7de7fd3eaece59bdadd8d7df411bee28_l3.png)
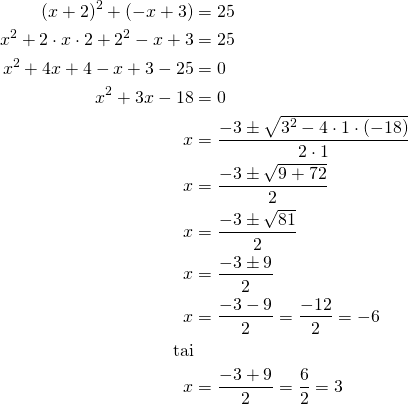
Ratkaistaan ![]() -koordinaattien arvot:
-koordinaattien arvot:
Kun ![]() ,
,
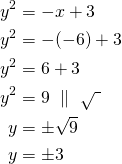
Kun ![]() ,
,
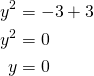
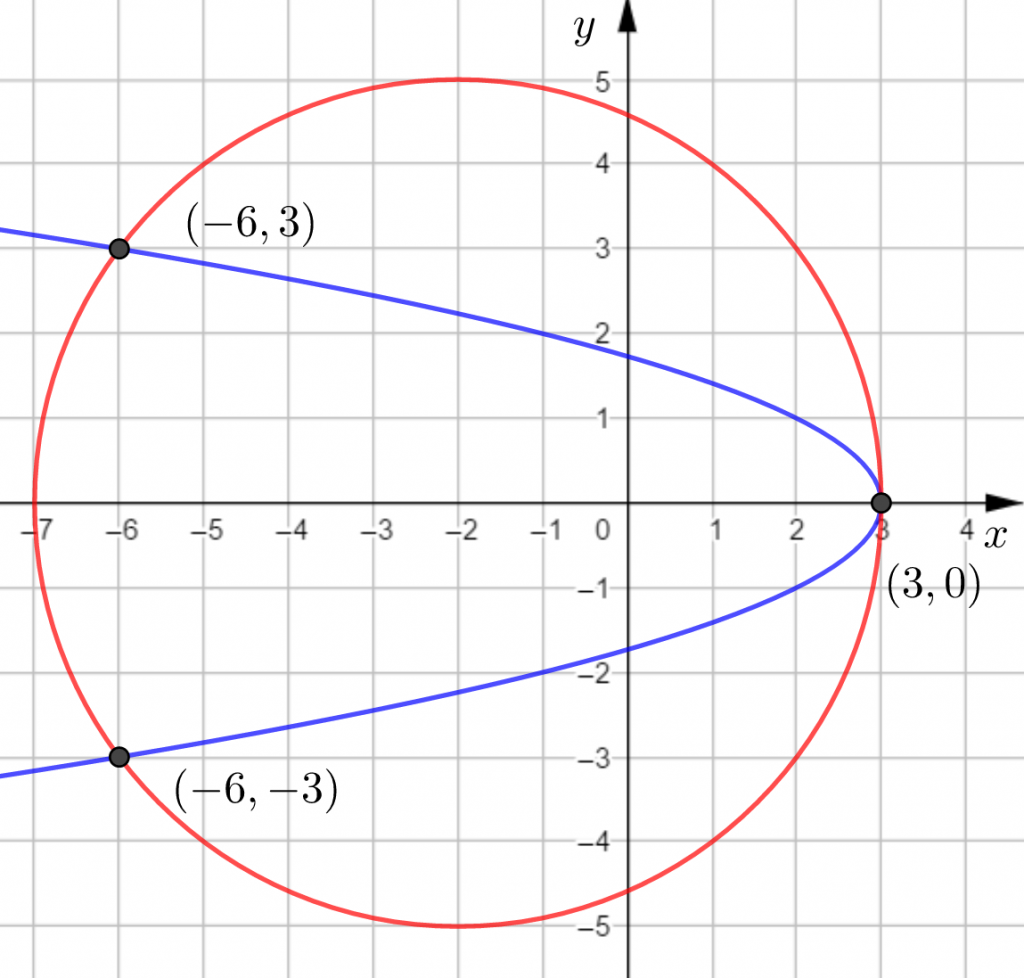
Kysytyt paraabelin pisteet ovat ![]() ,
, ![]() ja
ja ![]() .
.
Piirretään kuva GeoGebralla.
Olkoon piste ![]() kysytyllä käyrällä. Lasketaan sen etäisyys pisteestä
kysytyllä käyrällä. Lasketaan sen etäisyys pisteestä ![]() sekä
sekä ![]() -akselista, eli suorasta
-akselista, eli suorasta ![]() .
.
![]()
Koska etäisyydet ovat ei-negatiivisia, yhtälö voidaan korottaa puolittain toiseen.
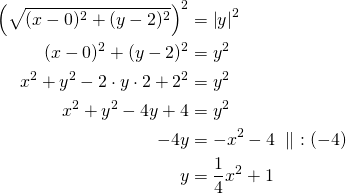
Suoran, joka kulkee pisteen ![]() kautta ja joka ei ole pystysuora, yhtälö on muotoa
kautta ja joka ei ole pystysuora, yhtälö on muotoa![]() eli
eli ![]() .
.
Suoralla ja paraabelilla on yksi yhteinen piste, kun yhtälöparilla
![Rendered by QuickLaTeX.com \[\begin{cases}y=x^2-6x+10\\y=kx-2k+1\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-6f46c61132f77e0c3d237e8e6c1800cd_l3.png)
on yksi ratkaisu.
Saadaan yhtälö
![]()
Siirretään kaikki termit vasemmalle puolelle.
![]()
![]()
Toisen asteen yhtälöllä ![]() on yksi ratkaisu, kun diskriminantti
on yksi ratkaisu, kun diskriminantti ![]() .
.
Lasketaan diskriminantti ![]()
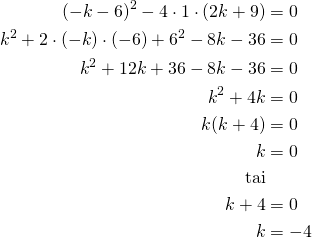
Kun suoran kulmakerroin ![]() tai
tai ![]() , niin suoralla ja paraabelilla on yksi yhteinen piste.
, niin suoralla ja paraabelilla on yksi yhteinen piste.
Suoralla ja paraabelilla on yksi yhteinen piste, kun suora on ![]() -akselin suuntainen, mutta tällöin suoralla ei ole kulmakerrointa.
-akselin suuntainen, mutta tällöin suoralla ei ole kulmakerrointa.
Vastaavasti kuin ![]() -kohdassa, mutta nyt pitää olla kaksi ratkaisua, joten diskriminantti
-kohdassa, mutta nyt pitää olla kaksi ratkaisua, joten diskriminantti ![]() .
.
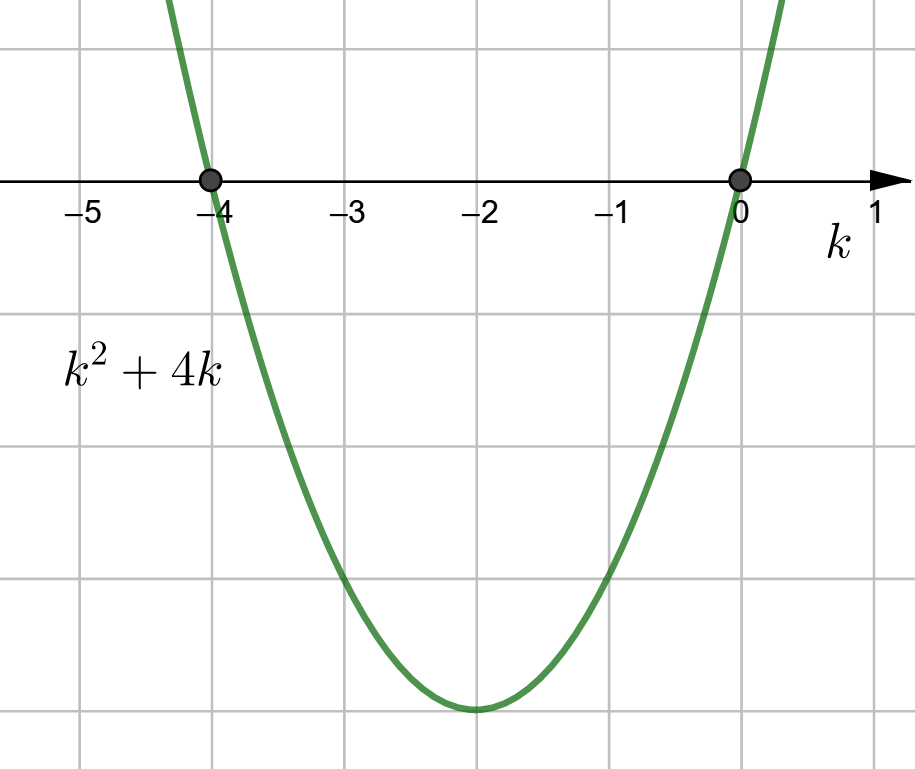
Epäyhtälön ![]() ratkaisu on
ratkaisu on ![]() tai
tai ![]() .
.