Viikon pistetehtävä
Ohjeistus:
- Ratkaise tehtävät välivaiheiden kanssa ilman teknisiä apuvälineitä.
- Tarkista lopuksi GeoGebralla.
- Kirjoita tehtävien ratkaisut math-demo.abitti.fi-sivuston kaavaeditorilla. Ota kuvakaappaukset kaavaeditorista ja GeoGebrasta ja liitä ne esimerkiksi Wordiin.
- Tallenna ratkaisut OneDrivessä minun kanssani jakamaasi kansioon nimellä ympyrätehtävä viimeistään sunnuntaina 26.9.2021 klo 23.59.
- Ympyrän yhtälö on
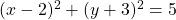 . Mitkä ovat ympyrän keskipiste ja säde?
. Mitkä ovat ympyrän keskipiste ja säde? - Määritä ympyrän
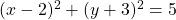 pisteeseen
pisteeseen 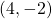 piirretyn tangentin yhtälö.
piirretyn tangentin yhtälö. - Onko edellä määrittämäsi tangentti myös ympyrän
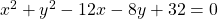 tangentti? Perustele laskemalla.
tangentti? Perustele laskemalla.
Tuntimuistiinpanot
Tuntitehtävät 441, 442, 444, 446
Ympyrän ![]() keskipiste on
keskipiste on ![]() ja säde on
ja säde on ![]() .
.
Lasketaan pisteen ![]() etäisyys suorasta
etäisyys suorasta ![]() .
.
Käytetään suoran yleisen muodon ![]() ja pisteen
ja pisteen ![]() etäisyyden laskemiseksi lauseketta
etäisyyden laskemiseksi lauseketta
![]()
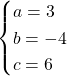
ja ![]()
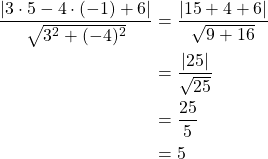
Suoran etäisyys ympyrän keskipisteestä on yhtä suuri kuin ympyrän säde, joten suora on ympyrän tangentti. Kuva II on oikea vaihtoehto.
Lasketaan ympyrän ![]() keskipisteen
keskipisteen ![]() etäisyys suorasta
etäisyys suorasta ![]() .
.
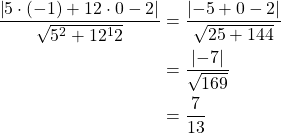
Ympyrän säde ![]() ja sen keskipisteen etäisyys suorasta on
ja sen keskipisteen etäisyys suorasta on ![]() , joten suoran etäisyys ympyrästä on pienempi kuin säde. Suora on ympyrän sekantti.
, joten suoran etäisyys ympyrästä on pienempi kuin säde. Suora on ympyrän sekantti.
Piste on ympyrällä, jos se toteuttaa ympyrän yhtälön. Sijoitetaan pisteen ![]() koordinaatit ympyrän
koordinaatit ympyrän ![]() yhtälöön.
yhtälöön.
![]() .
.
Siten piste on ympyrällä, koska se toteuttaa sen yhtälön.
Lasketaan keskipisteen ![]() ja sivuamispisteen
ja sivuamispisteen ![]() kautta kulkevan suoran kulmakerroin.
kautta kulkevan suoran kulmakerroin.
![]() .
.
Koska tangentti on kohtisuorassa sivuamispisteeseen piirrettyä sädettä vastaan ja siten myös tätä suoraa vastaan, niiden kulmakertoimien tulo on ![]() .
.
Tangentin kulmakerroin ![]() on
on
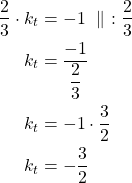
Määritetään tangentin yhtälö sijoittamalla suoran yhtälön kaavaan ![]() pisteeksi
pisteeksi ![]() ja
ja ![]()
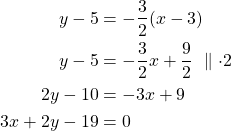
Katso kirjan appletti (https://www.geogebra.org/m/hyNBY8MQ#material/Q43cyhmn.)
Tangentteja on appletin perusteella kaksi ![]() ja
ja ![]() .
.
Koska tangentit ovat yhdensuuntaisia suoran ![]() kanssa, niiden kulmakertoimet ovat
kanssa, niiden kulmakertoimet ovat ![]() . Tangentin yhtälö on siis muotoa
. Tangentin yhtälö on siis muotoa ![]() , mikä yleisessä muodossa on
, mikä yleisessä muodossa on ![]() .
.
Ympyrän ![]() yhtälöstä saadaan suoraan ympyrän keskipiste
yhtälöstä saadaan suoraan ympyrän keskipiste ![]() ja säde
ja säde ![]() .
.
Tangentin etäisyys ympyrän keskipisteestä ![]() on ympyrän säde
on ympyrän säde ![]() .
.
Muodostetaan yhtälö, josta ratkaistaan vakio ![]() .
.
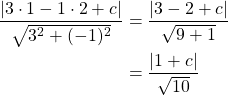
Tämä etäisyys on yhtä suuri kuin ![]() .
.
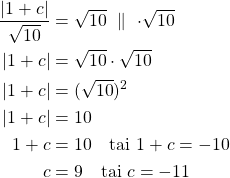
Kysytyt tangentit ovat ![]() ja
ja ![]() .
.
Kotitehtävät 443, 460.
Ympyrän säde on sama kuin sivuavan suoran ![]() ja ympyrän keskipisteen
ja ympyrän keskipisteen ![]() välinen etäisyys.
välinen etäisyys.
Käytetään suoran yleistä muotoa ![]() ja pisteen
ja pisteen ![]() etäisyyden lauseketta
etäisyyden lauseketta
![]()
![Rendered by QuickLaTeX.com \[r=\frac{\left|1 \cdot 4 + 2 \cdot 3 - 5\right|}{\sqrt{1^2+2^2}}=\frac{5}{\sqrt{1+4}}=^{ \sqrt{5} \text{)}}\frac{5}{\sqrt{5}}=\frac{\sqrt{5}\cdot5}{\left(\sqrt{5}\right)^2} =\frac{\sqrt{5}\cdot5}{5}= \sqrt{5}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-fd63007653552b21d86b50283059d0c6_l3.png)
Ympyrän keskipiste on ![]() ja säde on
ja säde on ![]() .
.
Ympyrän yhtälö on
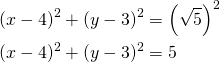
Tässä käy mikä tahansa ympyrä, joka sivuaa suoraa ![]() .
.
Määritetään esimerkiksi ympyrä, jonka keskipiste on origo ![]() . Lasketaan tällaisen ympyrän säde siten, että määritetään ympyrän, joka keskipiste on origossa, etäisyys suorasta
. Lasketaan tällaisen ympyrän säde siten, että määritetään ympyrän, joka keskipiste on origossa, etäisyys suorasta ![]() .
.
Pisteen ![]() etäisyys suorasta
etäisyys suorasta ![]() on
on ![]()
![]()
Ympyrän säde on siis ![]() .
.
Piirretään GeoGebralla ympyrä
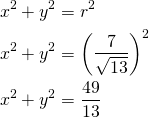
sekä suora ![]() , joka on yksi ympyrän tangentti.
, joka on yksi ympyrän tangentti.