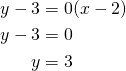Linkki tuntimuistiinpanohin.
Tuntitehtävät 442, 447, 451a, 452, 455a
Lasketaan ympyrän ![]() keskipisteen
keskipisteen ![]() etäisyys suorasta
etäisyys suorasta ![]() .
.
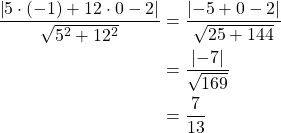
Ympyrän säde ![]() ja sen keskipisteen etäisyys suorasta on
ja sen keskipisteen etäisyys suorasta on ![]() , joten suoran etäisyys ympyrästä on pienempi kuin säde. Suora on ympyrän sekantti.
, joten suoran etäisyys ympyrästä on pienempi kuin säde. Suora on ympyrän sekantti.
Piirretään suora ![]() ja ympyrä
ja ympyrä ![]() GeoGebralla.
GeoGebralla.
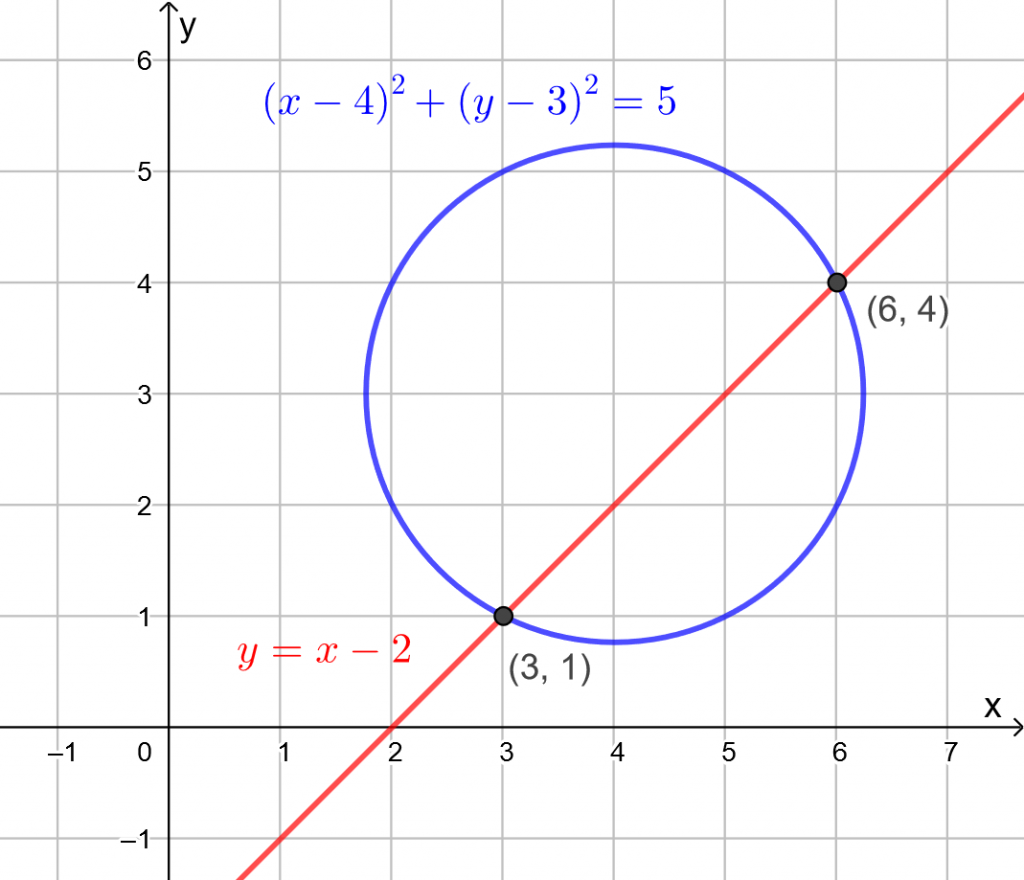
Kuvan perusteella suora ja ympyrä leikkaavat pisteissä ![]() ja
ja ![]() .
.
Ratkaistaan suoran ja ympyrän leikkauspisteet sijoitusmenetelmällä. Kirjoitetaan yhtälöpari.
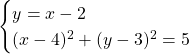
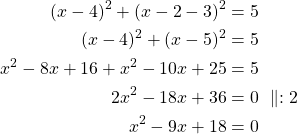
Ratkaistaan toisen asteen yhtälö, joka on muotoa ![]() , toisen asteen yhtälön ratkaisukaavalla:
, toisen asteen yhtälön ratkaisukaavalla:
![]()
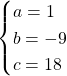
Sijoitetaan ![]() :n,
:n, ![]() :n ja
:n ja ![]() :n arvot ratkaisukaavaan:
:n arvot ratkaisukaavaan:
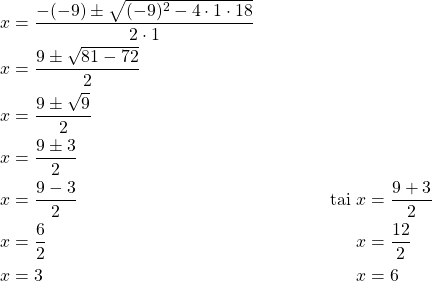
Leikkauspisteiden ![]() -koordinaatit saadaan sijoittamalla luvut
-koordinaatit saadaan sijoittamalla luvut ![]() ja
ja ![]() suoran yhtälöön
suoran yhtälöön ![]() .
.
Kun ![]() , niin
, niin ![]() .
.
Kun ![]() , niin
, niin ![]() .
.
Suoran ja ympyrän leikkauspisteet ovat ![]() ja
ja ![]() .
.
Sijoitetaan suoran yhtälöstä ![]() ympyrän yhtälöön
ympyrän yhtälöön ![]() .
.
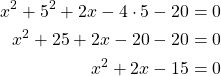
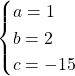

Koska suoran kaikille pisteillä ![]() , leikkaupisteet ovat
, leikkaupisteet ovat ![]() ja
ja ![]() .
.
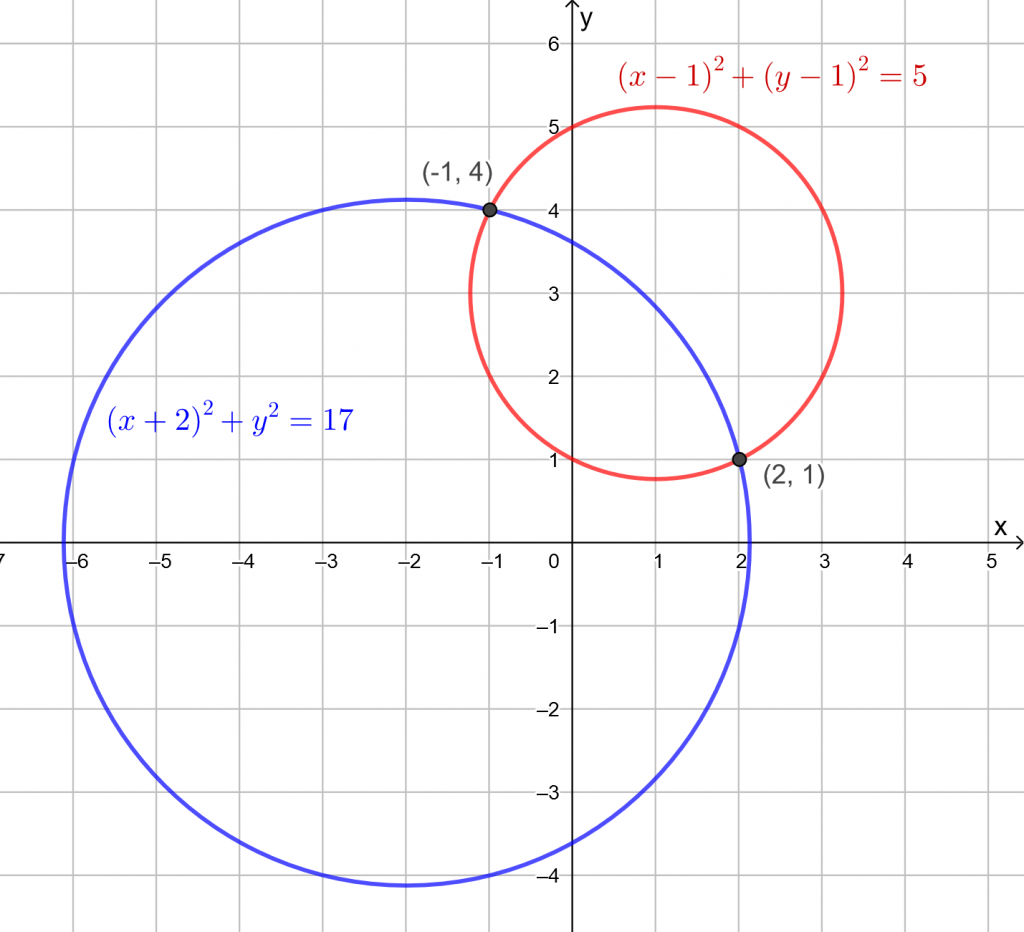
Piirretään kuva GeoGebralla.
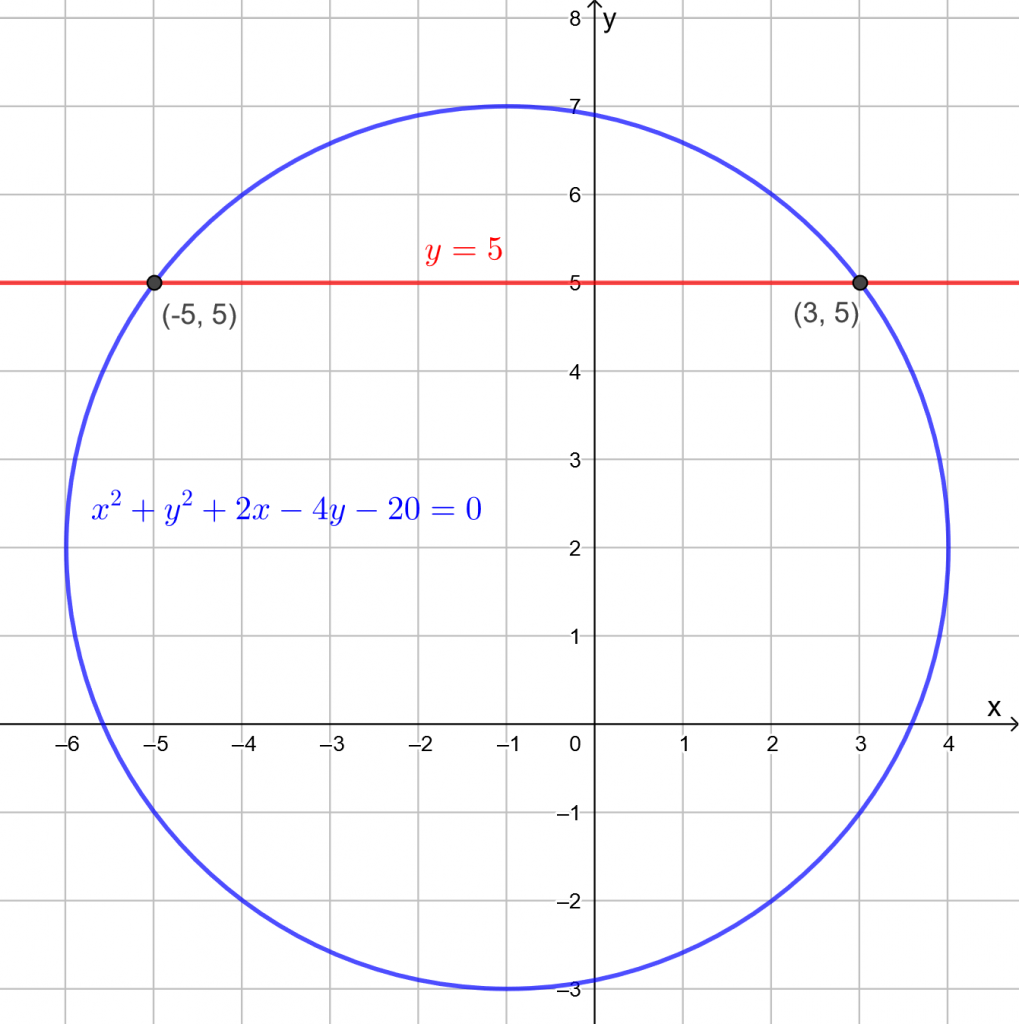
Ympyröiden leikkauspisteet saadaan ratkaisemalla seuraava yhtälöpari:
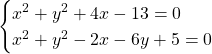
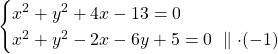
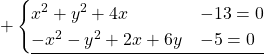
![]()
Ympyröiden leikkauspisteet ovat suoralla ![]() .
.
Ympyröiden leikkauspisteet saadaan ratkaisemalla suoran ja jomman kumman ympyrän yhtälön muodostama yhtälöpari.
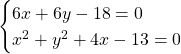
Kirjoitetaan suoran yhtälö ratkaistuun muotoon eli ratkaistaan siitä ![]() .
.
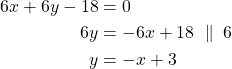
Sijoitetaan saatu ![]() :n lauseke ympyrän
:n lauseke ympyrän ![]() yhtälöön ja ratkaistaan
yhtälöön ja ratkaistaan ![]() .
.
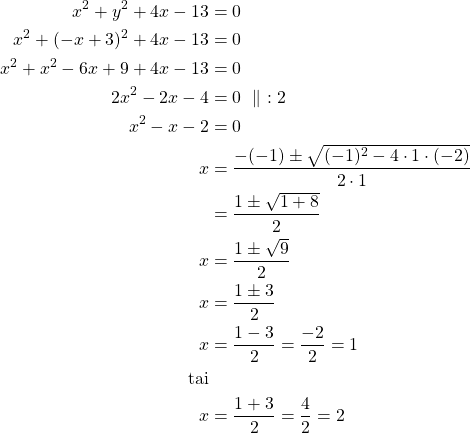
Leikkauspisteiden ![]() -koordinaatit ratkaistaan yhtälöstä
-koordinaatit ratkaistaan yhtälöstä ![]() .
.
Kun ![]() , niin
, niin ![]() .
.
Kun ![]() , niin
, niin ![]() .
.
Ympyrät leikkaavat pisteissä ![]() ja
ja ![]() .
.
Piirretään kuva GeoGebralla.
Ympyrän ![]() keskipistemuoto on
keskipistemuoto on ![]() .
.
Varmista, että osaat sen muodostaa.
Keskipiste on siis ![]() . Säde on
. Säde on ![]() .
.
Lasketaan pisteen ![]() etäisyys ympyrän keskipisteestä.
etäisyys ympyrän keskipisteestä.
![]() .
.
Koska etäisyys ![]() on suurempi kuin ympyrän säde
on suurempi kuin ympyrän säde ![]() , piste
, piste ![]() on ympyrän ulkopuolella.
on ympyrän ulkopuolella.
Piirretään kuva GeoGebralla.
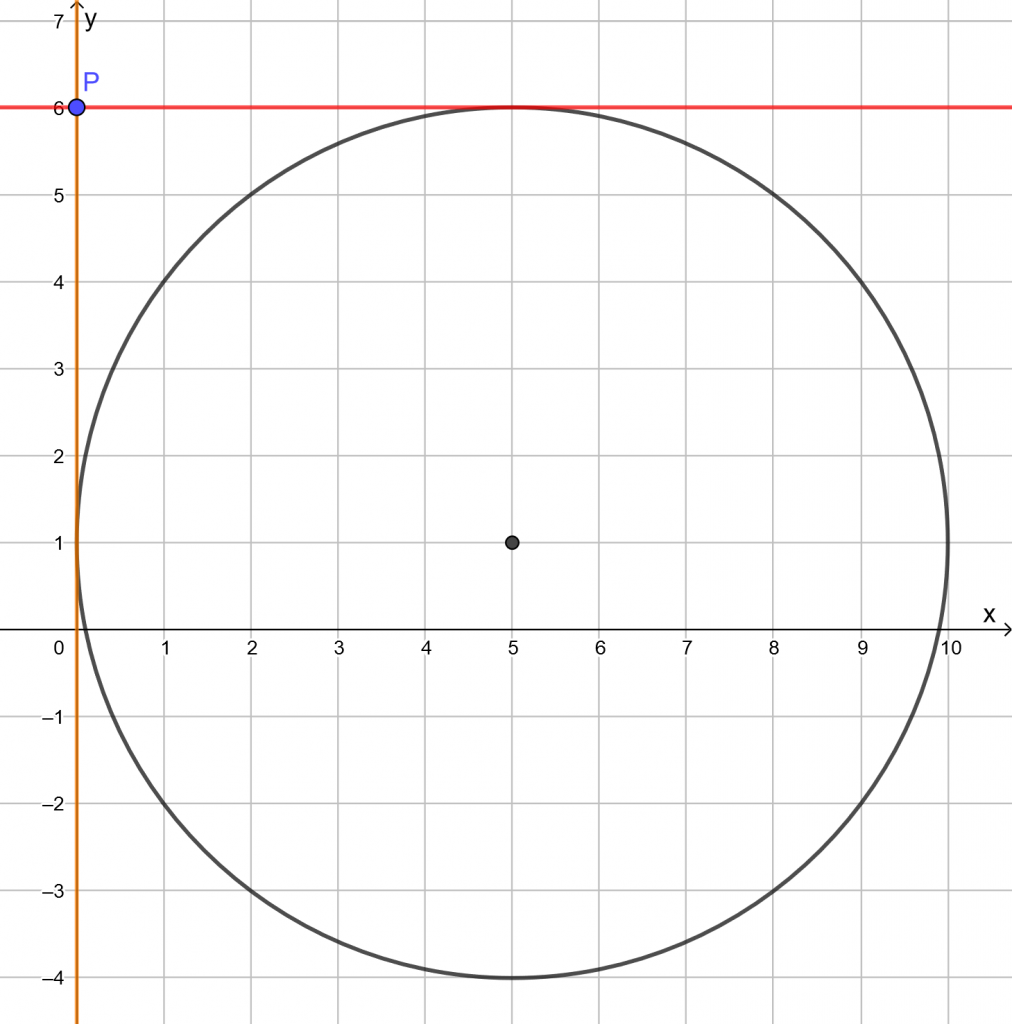
Ulkopuolisen pisteen kautta voidaan piirtää kaksi tangenttia ympyrälle.
Olkoon tangentin kulmakerroin ![]() . Tangentti kulkee pisteen
. Tangentti kulkee pisteen ![]() kautta.
kautta.
Muodostetaan tangentin yhtälö.
Tangentin etäisyys ympyrän keskipisteestä ![]() on ympyrän säteen suuruinen eli
on ympyrän säteen suuruinen eli ![]() .
.
Muodostetaan tangentin (siis suoran) etäisyyden lauskeke pisteeestä.
Yleisesti: Suoran ![]() etäisyys pisteestä
etäisyys pisteestä ![]() on
on
![]()
Nyt siis piste ![]() ja
ja
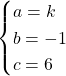
Sijoitetaan etäisyyden lausekkeeseen ja merkitään se yhtäsuureksi kuin säde ![]() .
.
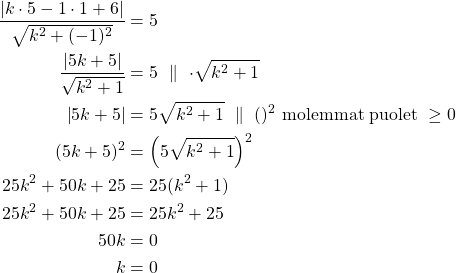
Ympyrällä on ei-pystysuora tangentti ![]() eli
eli ![]() .
.
Ympyrällä voi olla myös pystysuora tangentti. Koska tangentti kulkee pisteen ![]() kautta, ainoa mahdollinen pystysuora tangentti on suora
kautta, ainoa mahdollinen pystysuora tangentti on suora ![]() . Tämän etäisyys ympyrän keskipisteestä
. Tämän etäisyys ympyrän keskipisteestä ![]() on
on ![]() -koordinaattien etäisyys
-koordinaattien etäisyys ![]() , joka on yhtä suuri kuin ympyrän säde.
, joka on yhtä suuri kuin ympyrän säde.
Suora ![]() on siis myös ympyrän tangentti.
on siis myös ympyrän tangentti.
Vastaus: Pisteen ![]() kautta kulkevien ympyröiden tangenttien yhtälöt ovat
kautta kulkevien ympyröiden tangenttien yhtälöt ovat ![]() ja
ja ![]() .
.
Kotitehtävät 451b, 453, 461.
Suoran ![]() ja ympyrän
ja ympyrän ![]() leikkauspisteet.
leikkauspisteet.
Ratkaistaan suoran yhtälöstä ![]() . Sijoitetaan se ympyrän yhtälössä
. Sijoitetaan se ympyrän yhtälössä ![]() :n paikalle ja ratkaistaan
:n paikalle ja ratkaistaan ![]() .
.
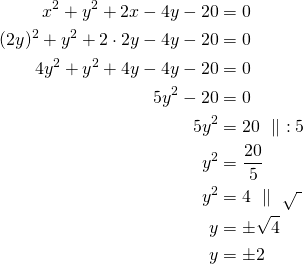
Ratkaistaan ![]() , kun
, kun ![]() ja
ja ![]() . Sijoitetaan
. Sijoitetaan ![]() :n arvot suoran yhtälöön.
:n arvot suoran yhtälöön.
Kun ![]() ,
, ![]() . Leikkauspiste on
. Leikkauspiste on ![]() .
.
Kun ![]() ,
, ![]() . Leikkauspiste on
. Leikkauspiste on ![]()
Piirretän GeoGebralla.
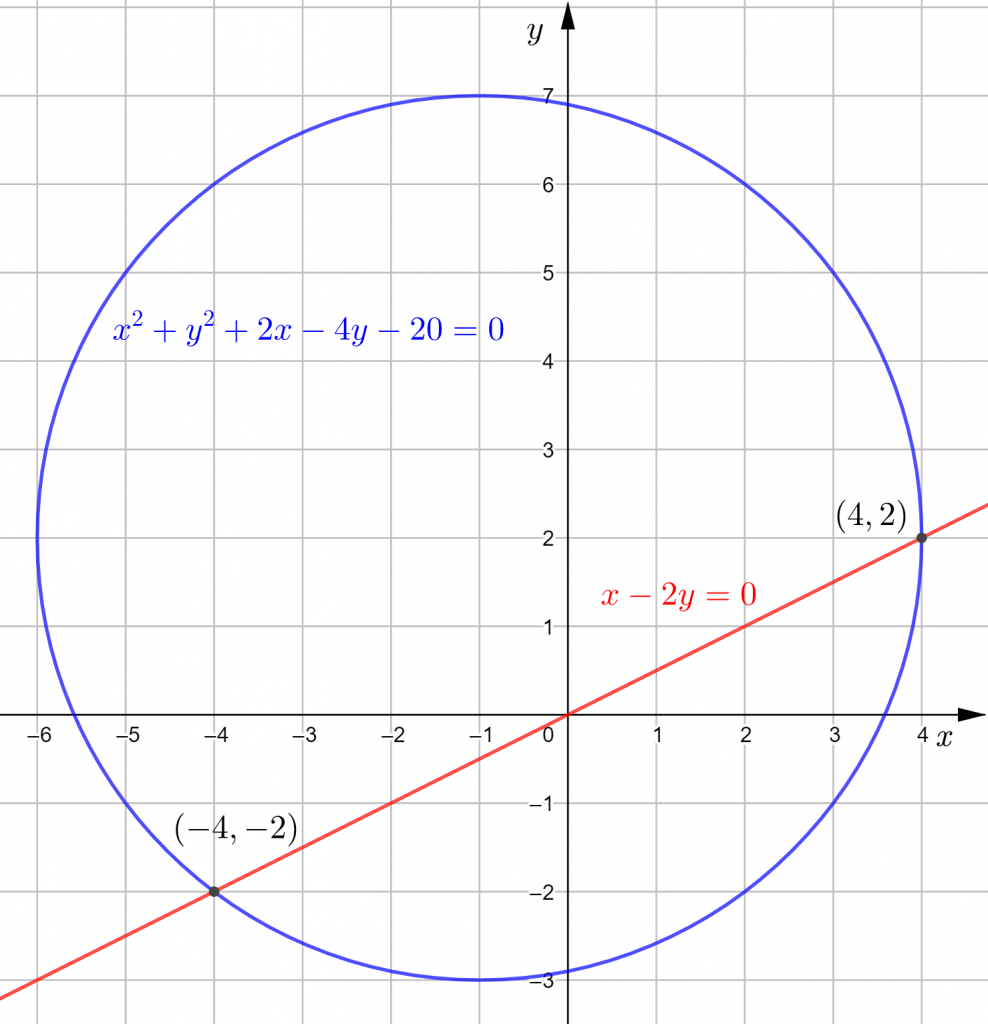
Ympyrän keskipiste on ![]() ja säde
ja säde ![]() .
.
Ympyrän keskipistemuoto on
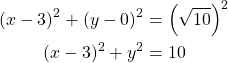
Ratkaistaan ![]() suoran yhtälöstä
suoran yhtälöstä ![]() , eli
, eli ![]() . Sijoitetaan tämä
. Sijoitetaan tämä ![]() :n paikalle ympyrän yhtälössä ja ratkaistaan
:n paikalle ympyrän yhtälössä ja ratkaistaan ![]() .
.
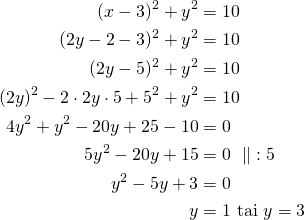
Ratkaise yllä oleva toisen asteen yhtälö vaikkapa GeoGebralla.
Ratkaistaan![]() :t arvot sijoittamalla suoran yhtälöön saadut
:t arvot sijoittamalla suoran yhtälöön saadut ![]() :n arvot.
:n arvot.
Kun ![]() ,
, ![]() .
.
Kun ![]() ,
, ![]() .
.
Leikkauspisteet ovat ![]() ja
ja ![]() .
.
Kirjoitetaan ympyrän keskipistemuoto normaalimuotoon.
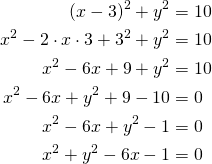
Ympyröiden leikkauspisteet saadaan alla olevan yhtälöparin ratkaisuista.
![Rendered by QuickLaTeX.com \[\begin{cases} x^2 +y^2 -6x -1=0 \\x^2+y^2-4x-2y-15=0\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-41870784e1e330a78e368740775a699a_l3.png)
Kerrotaan alempi yhtälö ![]() :llä lasketaan yhtälöt puolittain yhteen. Tällöin saadaan
:llä lasketaan yhtälöt puolittain yhteen. Tällöin saadaan
![Rendered by QuickLaTeX.com \[\begin{cases} x^2 +y^2 -6x -1=0 \\x^2+y^2-4x-2y-15=0\ \parallel\ \cdot (-1)\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-f5098da2ba8b9135195f2df46736a15f_l3.png)
![Rendered by QuickLaTeX.com \[+\begin{cases} &x^2 +y^2 -6x -1=0 \\-&x^2-y^2+4x+2y+15=0\\\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-a9e2cee9a54b401cecfad39cdf6abbc4_l3.png)
![]()
Ympyröiden leikkauspisteet ovat suoralla ![]() .
.
Ympyröiden leikkauspisteet saadaan suoran ja ympyrän ![]() yhtälöiden muodostamasta yhtälöparista.
yhtälöiden muodostamasta yhtälöparista.
![Rendered by QuickLaTeX.com \[\begin{cases} -2x + 2y + 14 = 0 \\x^2 +y^2 -6x -1=0 \\\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-99a65fec127a94b76e6d44be38e4ff3f_l3.png)
Ratkaistaan suoran yhtälöstä ![]() .
.
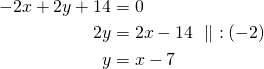
Sijoitetaan ![]() ympyrän
ympyrän ![]() yhtälöön ja ratkaistaan
yhtälöön ja ratkaistaan ![]() .
.
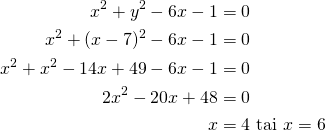
Ratkaise yllä oleva toisen asteen yhtälö esimerkiksi GeoGebralla.
Ratkaistaan leikkauspisteen ![]() -koordinaatit yhtälöstä
-koordinaatit yhtälöstä ![]() .
.
Kun ![]() , niin
, niin ![]() .
.
Kun ![]() , niin
, niin ![]() .
.
Ympyrät leikkaavat pisteissä ![]() ja
ja ![]() .
.
Piste ![]() on ympyrän ulkopuolella, koska sen etäisyys keskipisteeseen
on ympyrän ulkopuolella, koska sen etäisyys keskipisteeseen![]() on
on ![]() eli suurempi kuin säde
eli suurempi kuin säde ![]() .
.
Ulkopuolisen pisteen kautta voidaan piirtää kaksi tangenttia ympyrälle.
Pisteen ![]() kautta kulkevan, ei-pystysuoran tangentin yhtälö on muotoa
kautta kulkevan, ei-pystysuoran tangentin yhtälö on muotoa ![]() eli
eli ![]() .
.
Tangentin etäisyys ympyrän keskipisteestä (![]() on ympyrän säde
on ympyrän säde ![]() .
.
Muodostetaan yhtälö, josta ratkaistaan ![]() .
.
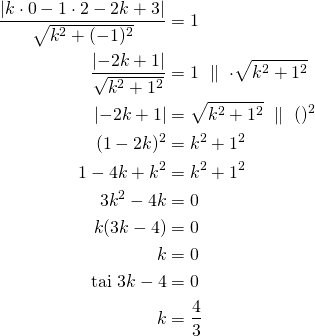
Tangentit ovat
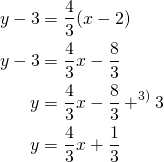
ja