Tunti- ja kotitehtävien ratkaisut 421, 422, 423, 425, 426, 427a, 431, 432, 433, 434, 436.
![]()
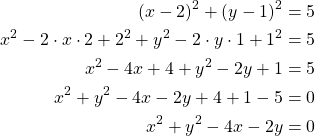
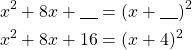
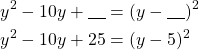
Puuttuvat luvut ovat 25 ja 5.
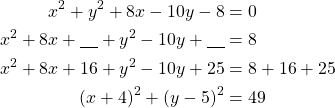
Kirjoitetaan ympyrän yhtälö keskipistemuotoon
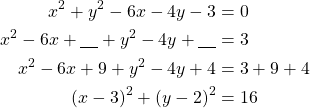
Ympyrän keskipiste on ![]() ja säde
ja säde ![]() .
.
Kirjoitetaan ympyrän yhtälö keskipistemuotoon.
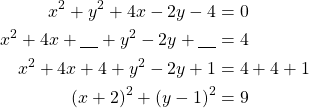
Ympyrän keskipiste on ![]() ja säde
ja säde ![]() .
.
Kirjoitetaan ympyrän yhtälö keskipistemuotoon.
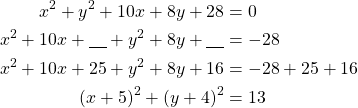
Ympyrän keskipiste on ![]() ja säde
ja säde ![]() .
.
Kirjoitetaan ympyrän yhtälö keskipistemuotoon.
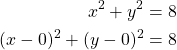
Ympyrän keskipiste on ![]() ja säde
ja säde ![]() .
.
Kirjoitetaan yhtälö keskipistemuotoon.
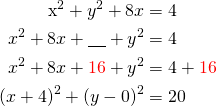
Kyseessä on ympyrä, jonka
- keskipiste on
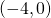 ja
ja - säde
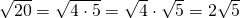 .
.
Kirjoitetaan yhtälö keskipistemuotoon.
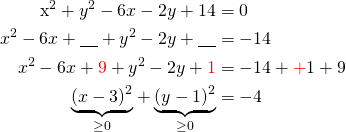
Kahden neliön summa ei voi olla negatiivinen, joten yhtälö ei esitä mitään käyrää.
Kirjoitetaan yhtälö keskipistemuotoon.
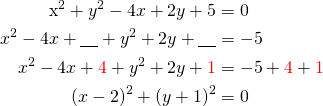
Kyseessä on piste ![]() .
.
Ympyrän keskipistemuoto on
![]()
Ympyrän
- keskipiste on
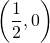 ja
ja - säde on
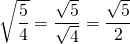 .
.
Kirjoitetaan yhtälö yleiseen muotoon:
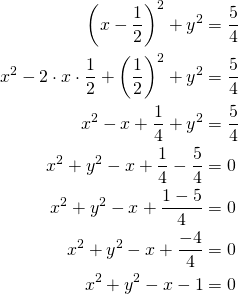
Ympyrän yhtälö yleisessä muodossa on ![]()
Kirjoitetaan yhtälö keskipistemuotoon.
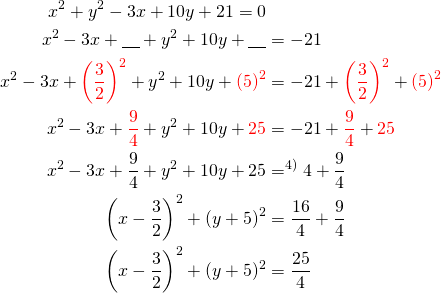
Ympyrän
- keskipiste on
 ja
ja - säde on
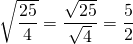 .
.
Ympyrän yhtälö yleisessä muodossa on ![]()
Kirjoitetaan yhtälö keskipistemuotoon.
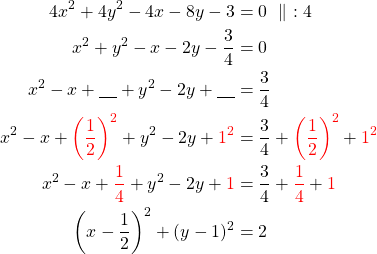
Kyseessä on ympyrä, jonka
- keskipiste on
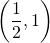 ja
ja - säde on
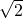 .
.
Ympyrän yhtälö yleisessä muodossa on ![]()
Kirjoitetaan yhtälö keskipistemuotoon.
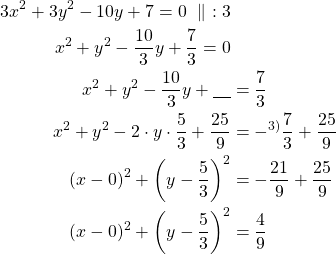
Kyseessä on ympyrä, jonka
- keskipiste on
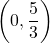 ja
ja - säde on
 .
.
Ympyrän yhtälö yleisessä muodossa on ![]()
Kirjoitetaan yhtälö keskipistemuotoon.
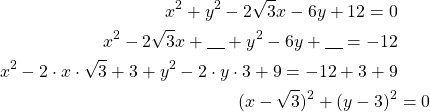
Yhtälö esittää pistettä ![]() .
.
Kirjoitetaan ympyröiden yhtälöt keskipistemuotoon.
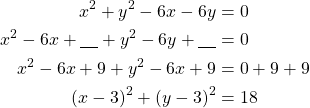
Ympyrän keskipiste on ![]() ja säde
ja säde ![]() .
.
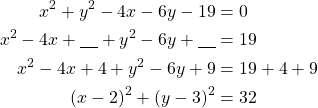
Ympyrän keskipiste on ![]() ja säde
ja säde ![]() .
.
Lasketaan ympyröiden keskipisteiden välinen etäisyys
![]() .
.
Koska ympyröiden keskipisteiden etäisyys on pienempi kuin kummankaan ympyrän säde, on toisen ympyrän keskipiste toisen ympyränä sisällä. Tällöin ympyrät joko leikkaavat toisiaan tai ovat sisäkkäin.
Alla on kuva tilanteessa GeoGebralla piirrettynä.
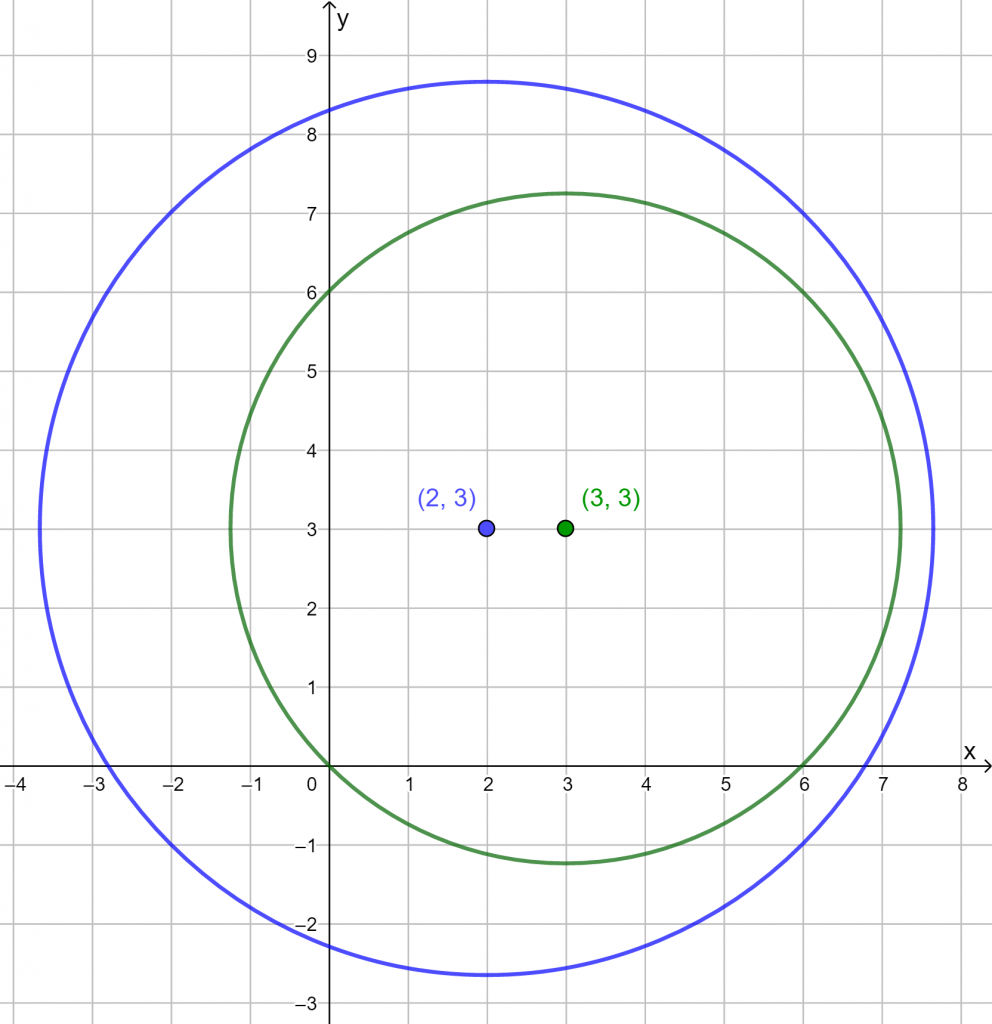
Pienemmän ympyrän pisteiden etäisyys sen keskipisteestä on ![]() . Koska ympyröiden keskipisteiden etäisyys on 1, on pienemmän ympyrän kehän
. Koska ympyröiden keskipisteiden etäisyys on 1, on pienemmän ympyrän kehän
pisteiden etäisyys isomman ympyrän keskipisteestä korkeintaan ![]() . Koska
. Koska ![]() , on tämä etäisyys aina pienempi kuin isomman ympyrän säde
, on tämä etäisyys aina pienempi kuin isomman ympyrän säde ![]() .
.
Pienempi ympyrä on isomman ympyrän sisässä.
Kun ympyrät sivuavat toisiaan, niiden keskipisteiden etäisyys on sama kuin säteiden summa.
Kirjoitetaan ympyrän yhtälö keskipistemuotoon.
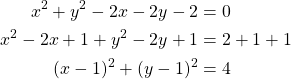
Ympyrän keskipiste on ![]() ja säde on
ja säde on ![]() .
.
Lasketaan pisteen ![]() etäisyys ympyrän
etäisyys ympyrän ![]() keskipisteestä
keskipisteestä ![]() .
.
![]()
Ympyröiden säteiden summa on ![]() . Siten toisen ympyrän säde on
. Siten toisen ympyrän säde on
![]() tai
tai ![]() .
.
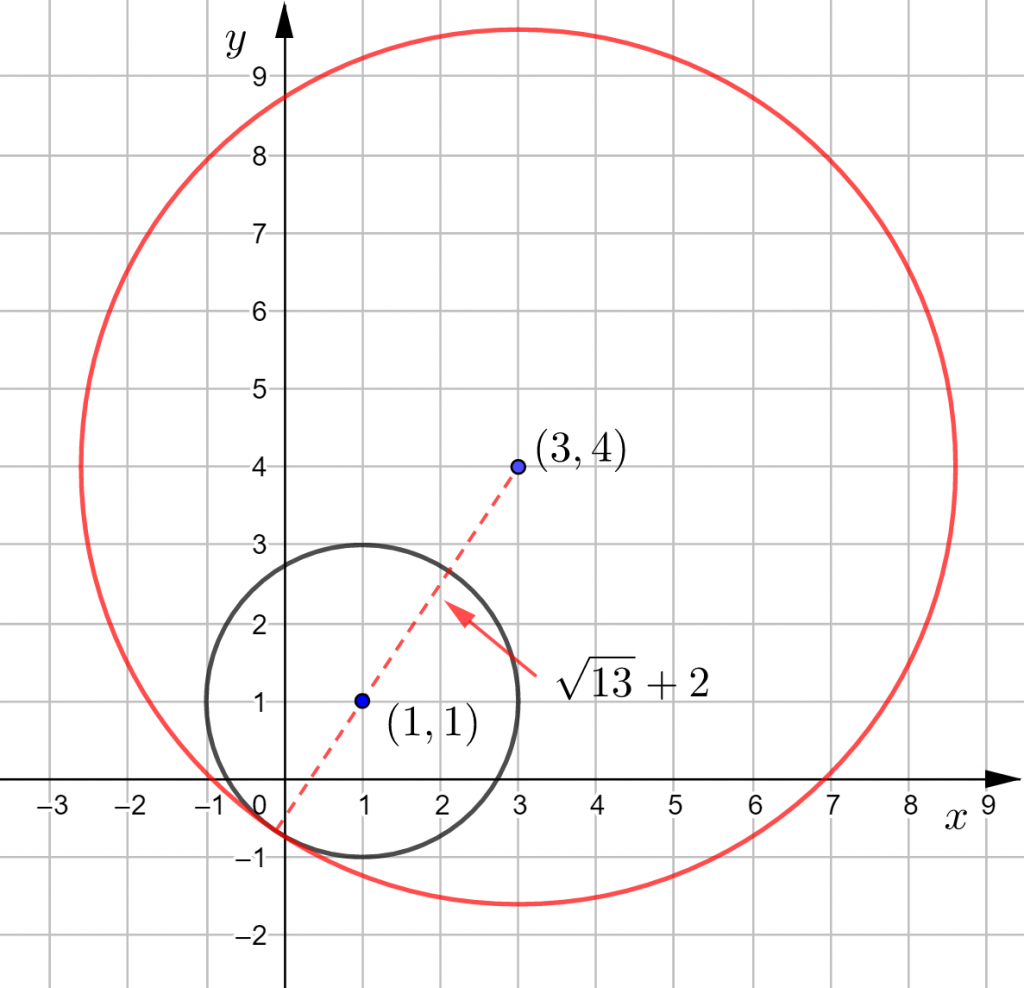
Piirretään kuva GeoGebralla. Tässä on siis kaksi mahdollisuutta:
- ympyrät eivät ole sisäkkäin, jolloin ympyrät sivuavat toisiaan tai
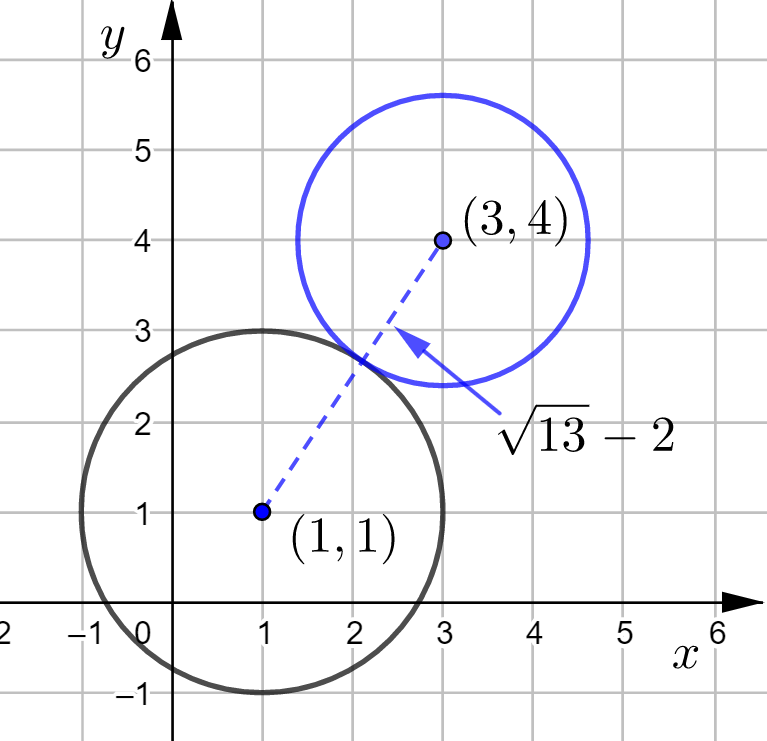
- ympyrä
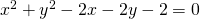 on ympyrän, jonka keskipiste on
on ympyrän, jonka keskipiste on 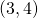 , sisällä.
, sisällä.
Ympyrän yhtälö yleisessä muodossa on ![]() . Koska ympyrä kulkee pisteiden
. Koska ympyrä kulkee pisteiden ![]() ,
, ![]() ja
ja ![]() kautta, ne toteuttavat ympyrän yhtälön.
kautta, ne toteuttavat ympyrän yhtälön.
Sijoitetaan kolmen pisteen ![]() -, ja
-, ja ![]() -koordinaatit ympyrän yleiseen lausekkeeseen. Tällöin saadaan kolme yhtälöä.
-koordinaatit ympyrän yleiseen lausekkeeseen. Tällöin saadaan kolme yhtälöä.
Piste ![]() :
:
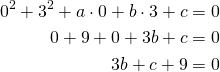
Piste ![]() :
:
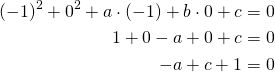
Piste ![]() :
:
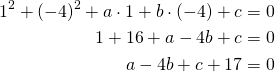
Saadaan kolmen yhtälön yhtälöryhmä.
![Rendered by QuickLaTeX.com \[\begin{cases} 3b+c+9=0 \\ -a+c+1=0 \\ a-4b+c+17=0\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-a35e7d2fcc729fa2d05d7c3180ad13fa_l3.png)
Ratkaistaan yhtälöryhmästä ![]() ,
, ![]() ja
ja ![]() GeoGebralla (CAS)
GeoGebralla (CAS)
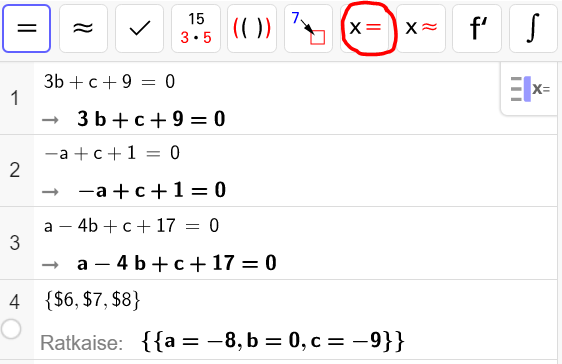
Ratkaisu on siis
![Rendered by QuickLaTeX.com \[\begin{cases} a=-8 \\ b=0 \\ c=-9\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-8c58f6f64aaa595dcb53e69cda18216e_l3.png)
Siten ympyrän yhtälö yleisessä muodossa on ![]()
Ympyrän yhtälö keskipistemuodossa on
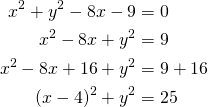
Ympyrän keskipiste on ![]() ja säde
ja säde ![]() .
.
Pisteet ovat saman ympyrän kehällä. Kysytty piste on ympyrän keskipiste.
Sijoitetaan pisteet ![]() ,
, ![]() ja
ja ![]() ympyrän yleiseen lausekkeeseen
ympyrän yleiseen lausekkeeseen ![]() .
.
Tällöin saadaan kolme yhtälöä.
Piste ![]() :
:
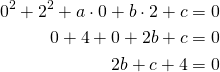
Piste ![]() :
:
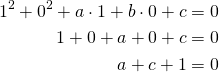
Piste ![]() :
:
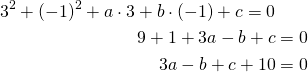
Saadaan kolmen yhtälön yhtälöryhmä.
![Rendered by QuickLaTeX.com \[\begin{cases} 2b+c+4=0 \\ a+c+1=0 \\ 3a-b+c+10=0\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-45293f319dc30ef1affef02b3334f423_l3.png)
Ratkaistaan yhtälöryhmästä ![]() ,
, ![]() ja
ja ![]() GeoGebralla (CAS)
GeoGebralla (CAS)
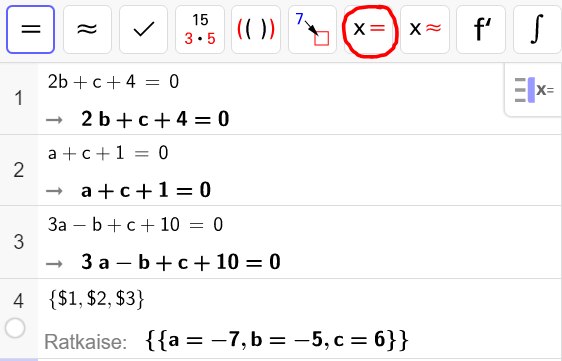
Ratkaisu on siis
![Rendered by QuickLaTeX.com \[\begin{cases} a=-7 \\ b=-5\\ c=6\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-5774aa7e33199e48b7f5618c9e424f0d_l3.png)
Siten ympyrän yhtälö yleisessä muodossa on ![]() .
.
Ympyrän yhtälö keskipistemuodossa on
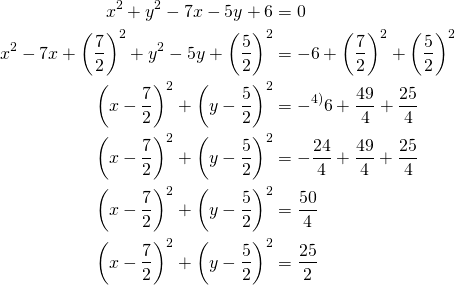
Ympyrän
- keskipiste on
 ja
ja - säde
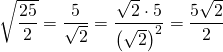
Vastaus: Pisteet ![]() ,
, ![]() ja
ja ![]() ovat säteen
ovat säteen ![]() etäisyydellä pisteestä
etäisyydellä pisteestä ![]() .
.
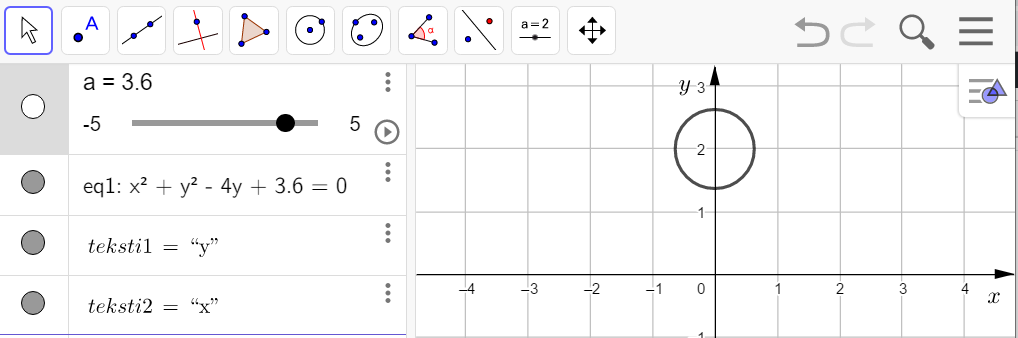
Piirretään yhtälö GeoGebralla.
Kokeillaan liukysäätimen eri arvoilla, milloin yhtälö ![]() esittää pistettä. Huomataan, että arvolla
esittää pistettä. Huomataan, että arvolla ![]() yhtälö esittää pistettä.
yhtälö esittää pistettä.
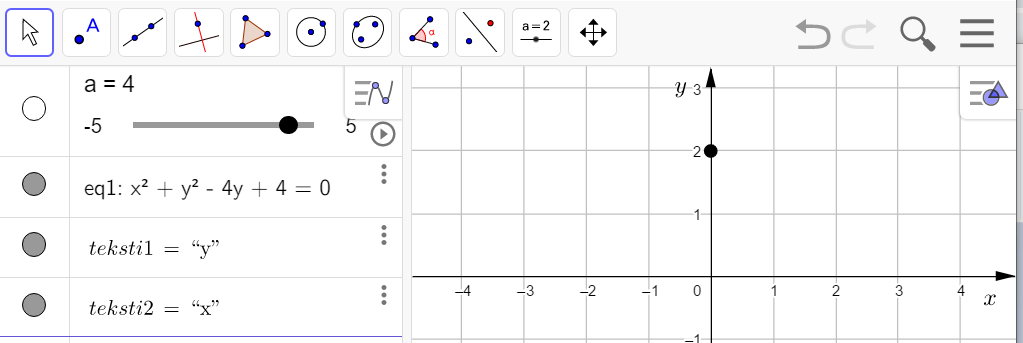
Yhtälö ![]() esittää ympyrää arvoilla
esittää ympyrää arvoilla ![]() .
.
Kirjoitetaan yhtälö ![]() keskipistemuotoon.
keskipistemuotoon.
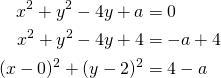
Yhtälö esittää pistettä ![]() , jos
, jos
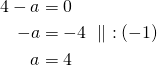
Yhtälö esittää ympyrää, jos
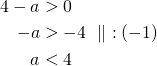
Tällöin keskipiste on ![]() ja säde
ja säde ![]() .
.