Tuntitehtävien 401, 402, 405, 407 ja 410 ratkaisut
Muodostetaan ympyrän yhtälö kaavalla
![]()
Kaavassa ympyrän keskipiste ![]() ja säde
ja säde ![]() .
.
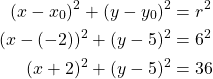
Muodostetaan ympyrän yhtälö kaavalla
![]()
Kaavassa ympyrän keskipiste ![]() ja säde
ja säde ![]() .
.
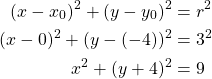
Muodostetaan ympyrän yhtälö kaavalla
![]()
Kaavassa ympyrän keskipiste ![]() ja säde
ja säde ![]() .
.
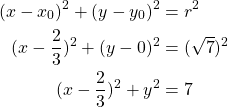
Kirjoitetaan yhtälö keskipistemuotoon, josta nähdään keskipiste ja säde
![]()
Keskipiste on ![]() ja säde 3.
ja säde 3.
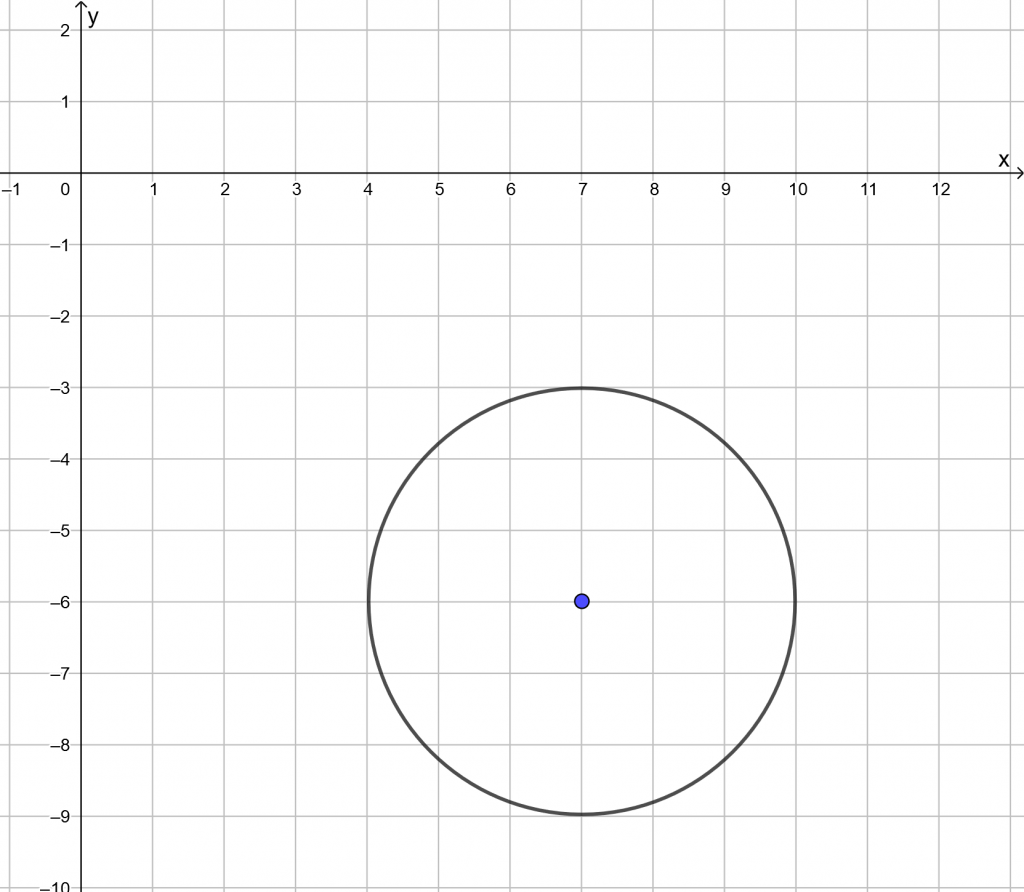
Kirjoitetaan yhtälö keskipistemuotoon, josta nähdään keskipiste ja säde
![]()
Keskipiste on ![]() ja säde
ja säde ![]() .
.
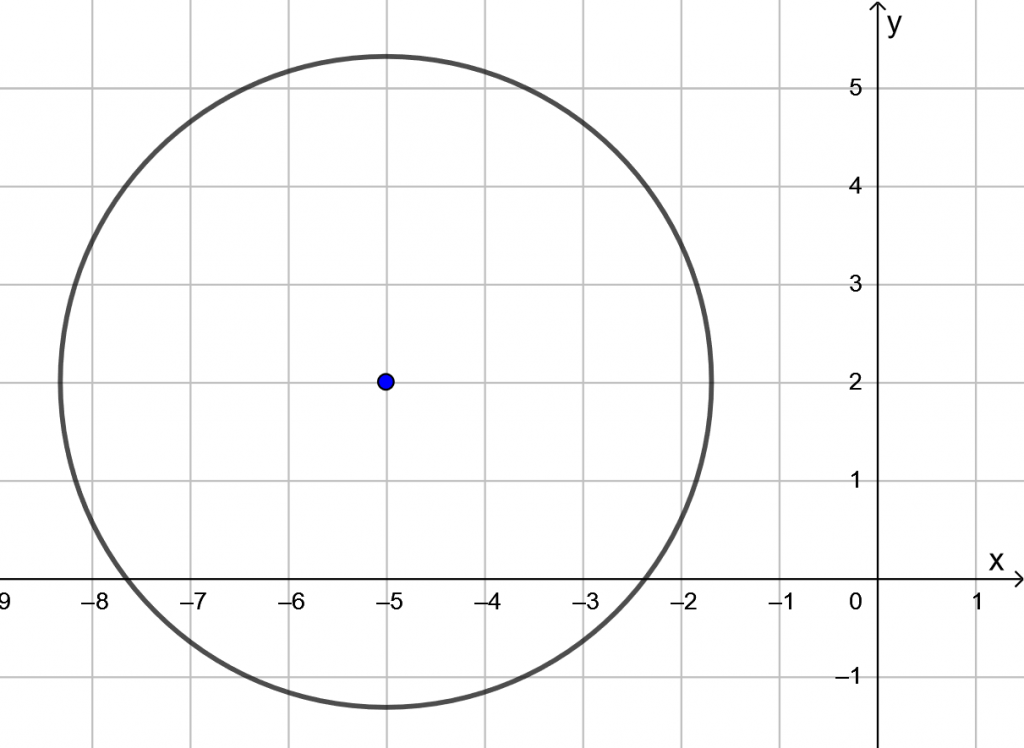
Kirjoitetaan yhtälö keskipistemuotoon, josta nähdään keskipiste ja säde
![]()
Keskipiste on ![]() ja säde
ja säde ![]() .
.
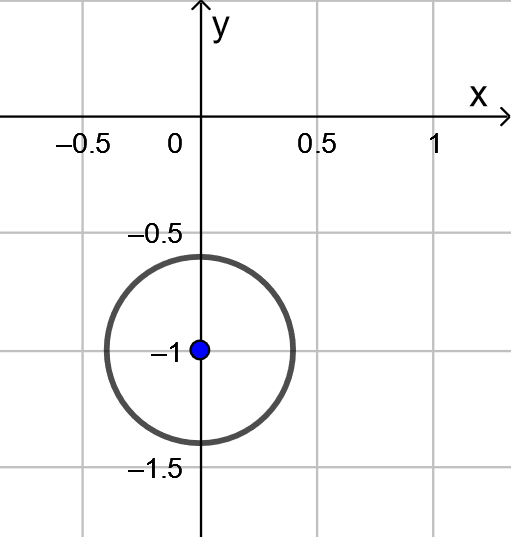
Lasketaan pisteen ![]() etäisyys ympyrän keskipisteestä
etäisyys ympyrän keskipisteestä ![]() .
.
![]() .
.
Koska pisteen ![]() etäisyys keskipisteestä on pienempi kuin säde
etäisyys keskipisteestä on pienempi kuin säde ![]() , piste
, piste ![]() on ympyrän sisäpuolella.
on ympyrän sisäpuolella.
Lasketaan pisteen ![]() etäisyys ympyrän keskipisteestä
etäisyys ympyrän keskipisteestä ![]() .
.
![]() .
.
Koska pisteen ![]() etäisyys keskipisteestä on sama kuin säde
etäisyys keskipisteestä on sama kuin säde ![]() , piste
, piste ![]() on ympyrällä.
on ympyrällä.
Lasketaan pisteen ![]() etäisyys ympyrän keskipisteestä
etäisyys ympyrän keskipisteestä ![]() .
.
![]() .
.
Koska pisteen ![]() etäisyys keskipisteestä on suurempi kuin säde
etäisyys keskipisteestä on suurempi kuin säde ![]() , piste
, piste ![]() on ympyrän ulkopuolella.
on ympyrän ulkopuolella.
Ympyrän keskipiste on halkaisijan keskipiste eli
![]() .
.
Ympyrän säde on keskipisteen etäisyys halkaisijan päätepisteeseen.
Lasketaan keskipisteen ![]() ja pisteen
ja pisteen ![]() etäisyys.
etäisyys.
![]() .
.
Ympyrän yhtälö on
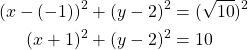
Neliön keskipiste on ![]() ja yksi kärkipiste on
ja yksi kärkipiste on ![]() . Muut kärkipisteet ovat
. Muut kärkipisteet ovat ![]() ,
, ![]() ja
ja ![]() .
.
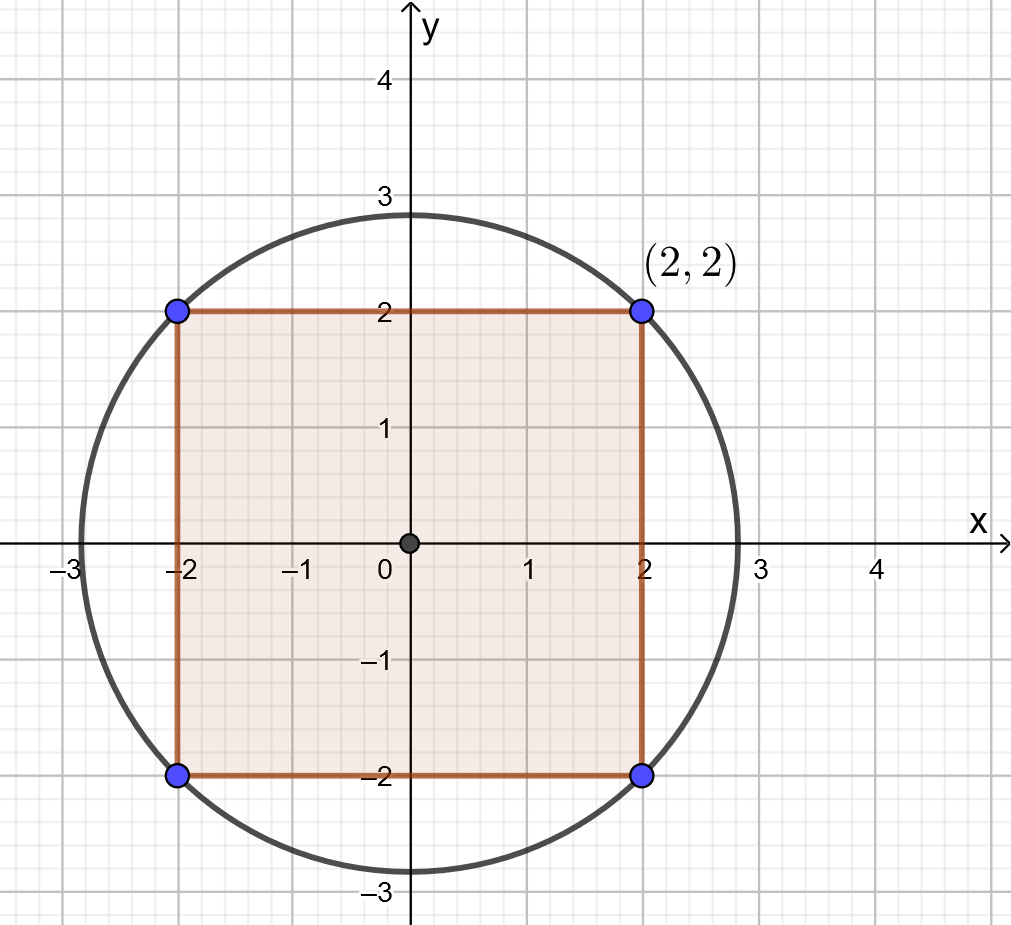
Ympyrän keskipiste on sama kuin neliön keskipiste eli origo ![]() .
.
Ympyrän yksi kehäpiste on neliön kärki ![]() . Ympyrän säde on kehäpisteen etäisyys keskipisteestä.
. Ympyrän säde on kehäpisteen etäisyys keskipisteestä.
![]()
Muodostetaan ympyrän yhtälö. Keskipiste on ![]() ja säde
ja säde ![]() .
.
![]()
Neliön sivun pituus on ![]() , joten sen pinta-ala on
, joten sen pinta-ala on ![]() .
.
Ympyrän pinta-ala on ![]() .
.
Neliön ja ympyrän pinta-alojen suhde on
![]() .
.
Kotitehtävien 403, 409, 413, 417 ratkaisut.
Ympyrän keskipiste ![]() ja piste, jonka kautta ympyrä kulkee on,
ja piste, jonka kautta ympyrä kulkee on, ![]() .
.
Muodostetaan ympyrän yhtälö kaavalla
![]()
Kaavassa ympyrän keskipiste ![]() ja ympyrän säde
ja ympyrän säde ![]() on a)-kohdassa laskettu
on a)-kohdassa laskettu ![]() .
.
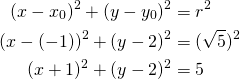
Ympyrän säde on pisteiden ![]() ja
ja ![]() välinen etäisyys
välinen etäisyys ![]() eli
eli
![]() .
.
Osoitetaan väite todeksi sijoittamalla pisteen ![]() koordinaatit ympyrän yhtälöön:
koordinaatit ympyrän yhtälöön:
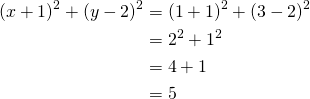
Koska ympyrän yhtälö toteutuu, piste ![]() on ympyrällä.
on ympyrällä.
SIjotetaan pisteen ![]() koordinaatit ympyrän yhtälöön ja tutkitaan toteutuuko yhtälö.
koordinaatit ympyrän yhtälöön ja tutkitaan toteutuuko yhtälö.
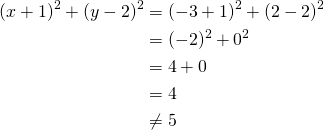
Koske ympyrän yhtälö ei toteudu, piste ![]() ei ole ympyrällä.
ei ole ympyrällä.
Ympyrän ![]() keskipiste on
keskipiste on ![]() ja säde
ja säde ![]() .
.
Ympyrän ![]() keskipiste on
keskipiste on ![]() ja säde
ja säde ![]() .
.
Piirretään ympyrät GeoGebralla.
- Tee ympyrät toiminnolla Ympyrä: Keskipiste ja Säde. Valitse keskipiste ja anna säteen suuruus. Neliöjuuren saat virtuaalinäppäimistöltä tai kirjoittamalla \sqrt(8).
- Määritä jana keskipisteiden välille.
- Määritä keskipisteiden välisen janan ja kummankin ympyrän leikkauspisteet.
- Määritä jana leikkaupisteiden välille.
- Mittaa sen pituus.
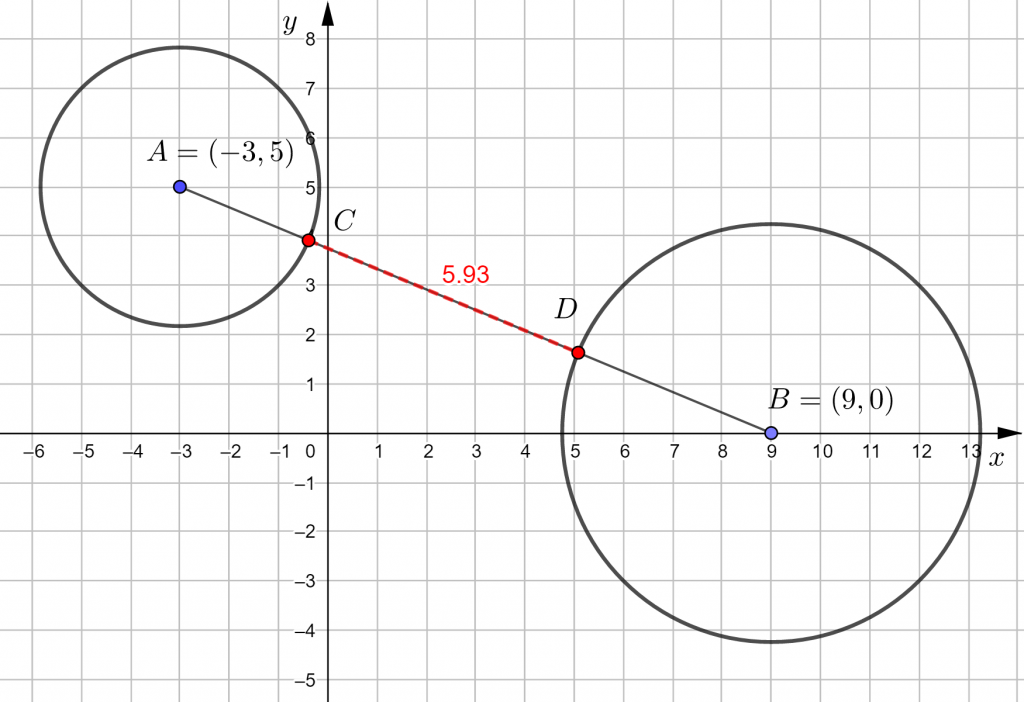
Ympyröiden välinen etäisyyden määrittämiseksi lasketaan ensin ympyröiden keskipisteiden etäisyys. Kun tästä vähennetään ympyröiden säteet (![]() ja
ja ![]() ) saadaan ympyröiden etäisyys.
) saadaan ympyröiden etäisyys.
Keskipisteiden välinen etäisyys eli pisteiden ![]() ja
ja ![]() välinen etäisyys on
välinen etäisyys on
![]()
Ympyröiden välinen etäisyys on
![]()
Pisteet ovat ympyrällä, jos ne toteuttavat ympyrän yhtälön ![]() .
.
Piste ![]() :
:
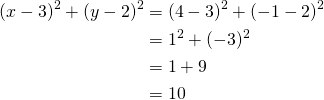
Koska ympyrän yhtälö toteutuu, piste ![]() on ympyrällä.
on ympyrällä.
Piste ![]() :
:
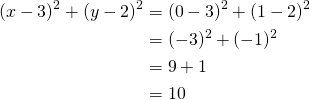
Koska ympyrän yhtälö toteutuu, piste ![]() on ympyrällä.
on ympyrällä.
Piste ![]() :
:
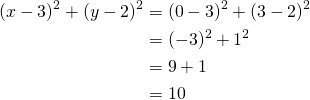
Koska ympyrän yhtälö toteutuu, piste ![]() on ympyrällä.
on ympyrällä.
Piirretään ympyrä ![]() . Ympyrän keskipiste on
. Ympyrän keskipiste on ![]() ja säde on
ja säde on ![]() .
.
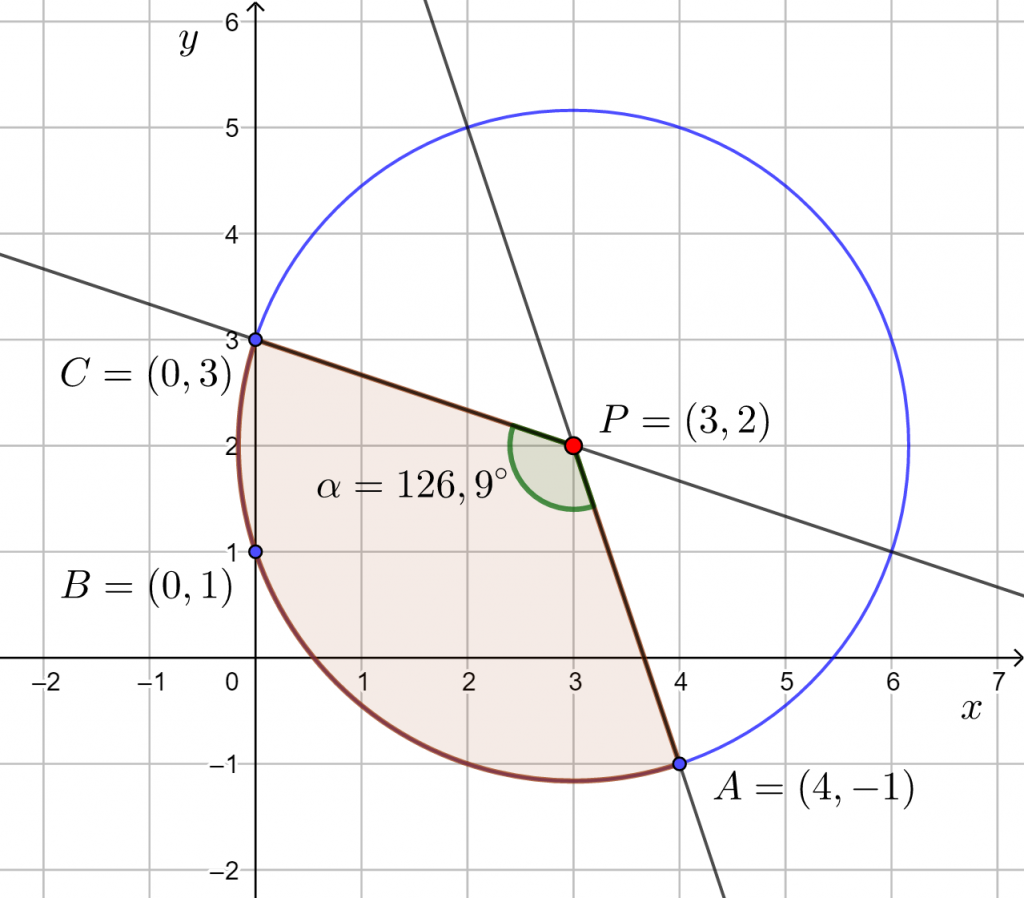
Ympyrän kaarta ![]() vastaava keskuskulma saadaan pisteiden
vastaava keskuskulma saadaan pisteiden ![]() ja
ja ![]() sekä
sekä ![]() ja
ja ![]() kautta kulkevien suorien välisen kulman avulla.
kautta kulkevien suorien välisen kulman avulla.
Pisteiden ![]() ja
ja ![]() välisen suoran kulmakerroin on
välisen suoran kulmakerroin on
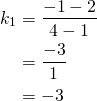
Pisteiden ![]() ja
ja ![]() välisen suoran kulmakerroin on
välisen suoran kulmakerroin on
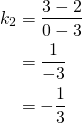
Suorien välinen kulma saadaan suuntakulman avulla:
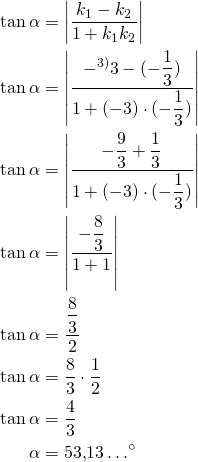
Ratkaisuna saatiin suorien välinen terävä kulma. Kuvion perusteella kulma on tylppä, joten kaarta ![]() vastaava keskuskulma on
vastaava keskuskulma on
![]() .
.
Kehäkulma on puolet vastaavasta keskuskulmasta, joten kehäkulmaksi saadaan
![]() .
.
Piirretään GeoGebralla suora ![]() . Ympyrä kulkee pisteiden
. Ympyrä kulkee pisteiden ![]() ja
ja ![]() kautta.
kautta.
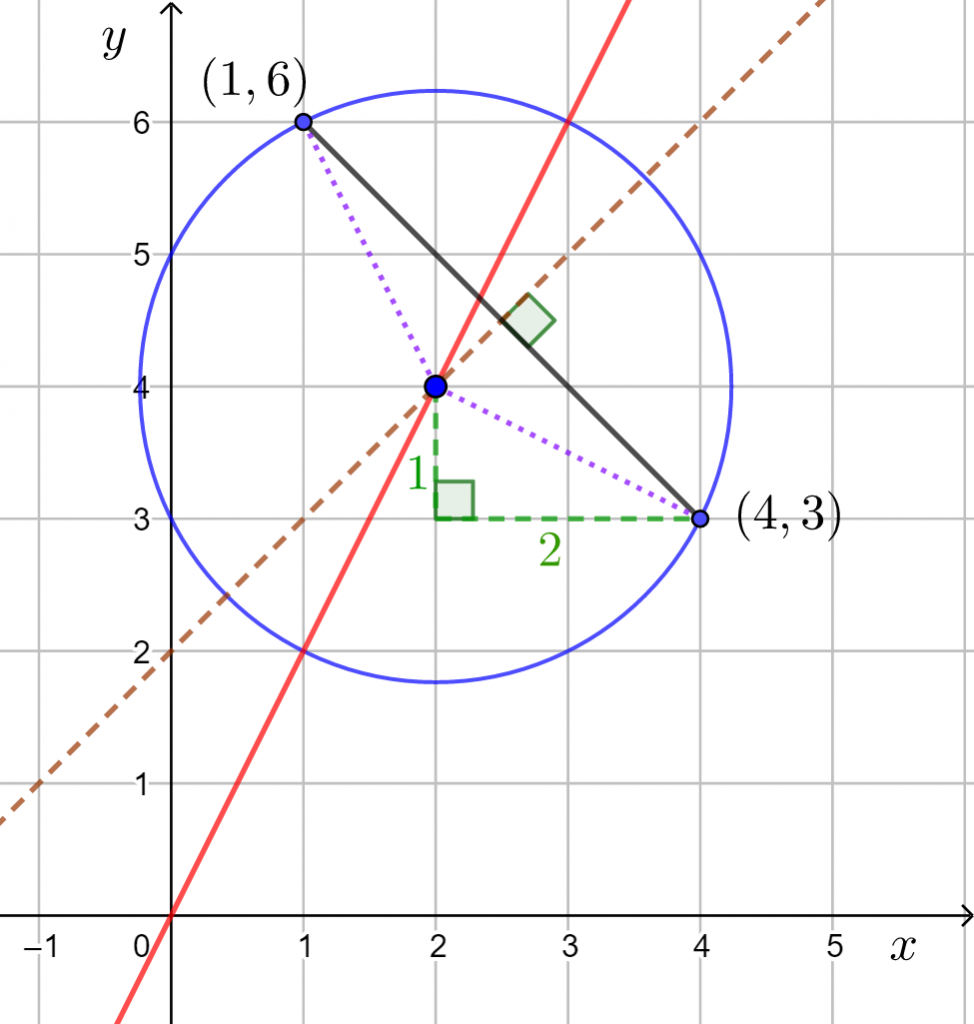
Ympyrän keskipiste, joka on suoralla ![]() , on yhtä kaukana kummastakin annetusta kehän pisteestä.
, on yhtä kaukana kummastakin annetusta kehän pisteestä.
Kehän pisteiden ![]() ja
ja ![]() välisen janan keskinormaalin jokainen piste on
välisen janan keskinormaalin jokainen piste on
yhtä kaukana janan molemmista päätepisteistä. Ympyrän keskipiste on
janan keskinormaalin ja suoran ![]() leikkauspisteessä.
leikkauspisteessä.
Piiroksen perusteella ympyrän keskipiste näyttäisi olevan pisteessä ![]() . Ympyrän säde sen perusteella (Pythagoraan lause) on
. Ympyrän säde sen perusteella (Pythagoraan lause) on
![]() .
.
Koska ympyrän keskipiste on suoralla ![]() , sen koordinaatit ovat (esimerkiksi merkittynä
, sen koordinaatit ovat (esimerkiksi merkittynä ![]() )
) ![]() . Kehän pisteiden
. Kehän pisteiden ![]() ja
ja ![]() etäisyys keskipisteestä
etäisyys keskipisteestä ![]() täytyy olla yhtä suuri.
täytyy olla yhtä suuri.
Täten saadaan etäisyydelle yhtälö:
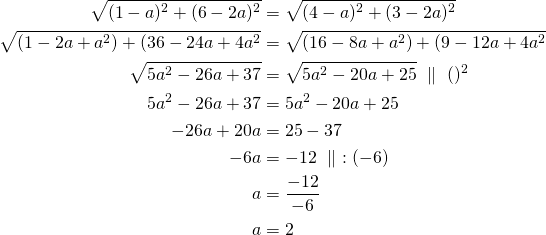
Ratkaisuna saatiin ![]() -koordinaatiksi
-koordinaatiksi ![]() , joten
, joten ![]() . Keskipiste on siten
. Keskipiste on siten ![]() .
.
Ympyrän säde ![]() on keskipisteen
on keskipisteen ![]() etäisyys kumpaan tahansa annettuun kehän pisteeseen, vaikkapa pisteeseen
etäisyys kumpaan tahansa annettuun kehän pisteeseen, vaikkapa pisteeseen ![]() :
:![]() .
.
Ympyrän yhtälöksi saadaan keskipisteen ![]() ja säteen
ja säteen ![]() avulla
avulla
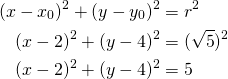
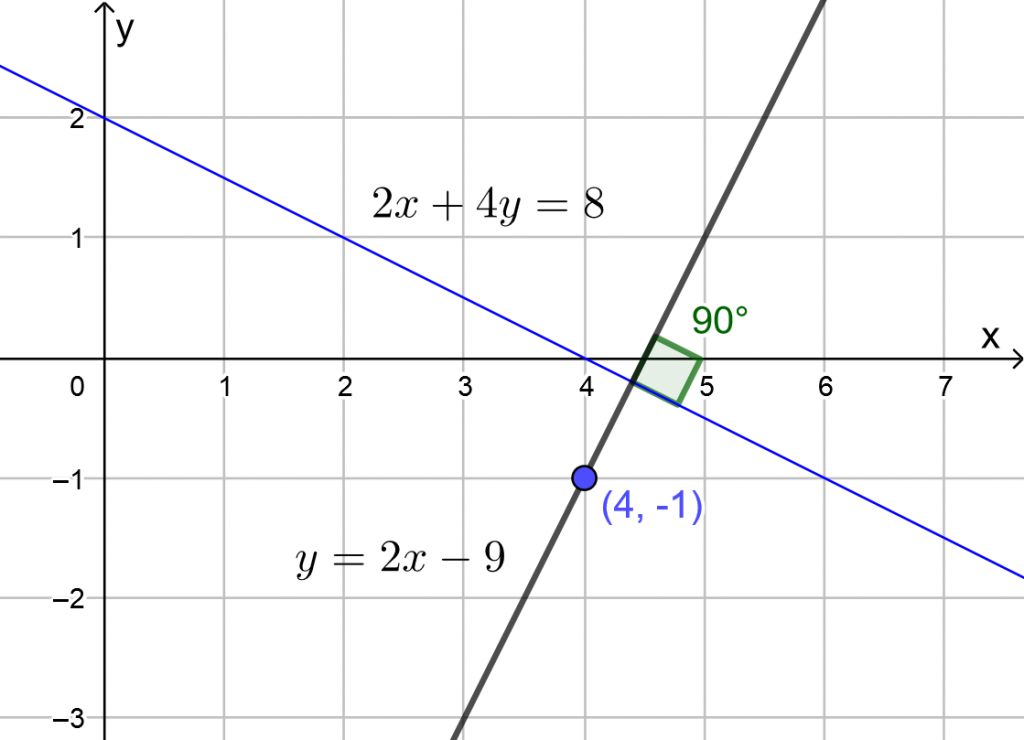
Lisäpistetehtävä 10.9.2020
Suoran ![]() yhtälö on
yhtälö on ![]() .
.
a) Mikä on suoran ![]() kulmakerroin.
kulmakerroin.
b) Mikä on suoraa ![]() vastan kohtisuorassa olevan suoran
vastan kohtisuorassa olevan suoran ![]() kulmakerroin?
kulmakerroin?
c) Muodosta suoran ![]() yhtälö, kun se kulkee pisteen
yhtälö, kun se kulkee pisteen ![]() kautta.
kautta.
d) Piirrä kuva GeoGebralla ja tarkista vastaukset. Ota kuvakaappaukset.
Ratkaisu
a) Muutetaan suoran ![]() yhtälö ratkaistuun muotoon:
yhtälö ratkaistuun muotoon:
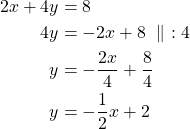
Vastaus: Suoran ![]() kulmakerroin on
kulmakerroin on ![]() .
.
b) Koska suora ![]() on kohtisuorassa suoraa
on kohtisuorassa suoraa ![]() vastaan, niin niiden kulmakertoimien tulo on
vastaan, niin niiden kulmakertoimien tulo on ![]() .
.
Siten
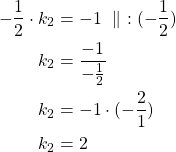
Vastaus: Suoran ![]() kulmakerroin on
kulmakerroin on ![]() .
.
c) Suoran, jonka kulmakerroin on ![]() ja se kulkee pisteen
ja se kulkee pisteen ![]() kautta, yhtälö muodostetaan kaavalla
kautta, yhtälö muodostetaan kaavalla
![]()
Siten
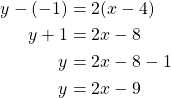
Vastaus: Suoran ![]() yhtälö on
yhtälö on ![]() .
.
d) Kuvat GeoGebralla.