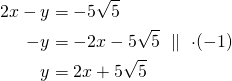Tuntitehtävät 370, 371, 372, 373, 374
Molempien suorien kulmakerroin on 2, joten suorat ovat yhdensuuntaiset.
Suorien kulmakertoimien tulo ![]() , joten suorat ovat kohdisuorassa.
, joten suorat ovat kohdisuorassa.
Suora ![]() on
on ![]() -akselin suuntainen suora ja suora
-akselin suuntainen suora ja suora ![]() on
on ![]() -akselin suuntainen, joten ne ovat kohtisuorassa toisiaan vastaan.
-akselin suuntainen, joten ne ovat kohtisuorassa toisiaan vastaan.
Merkitään suoran ![]() ja sen normaalin
ja sen normaalin ![]() kulmakeroiminen tulo yhtäsuureksi kuin -1:
kulmakeroiminen tulo yhtäsuureksi kuin -1:
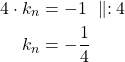
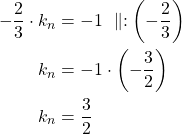
Suoran ![]() suuntakulma on
suuntakulma on ![]() , joten se on
, joten se on ![]() -akselin suuntainen. Sen normaali on
-akselin suuntainen. Sen normaali on ![]() -akselin suuntainen, joten suoran
-akselin suuntainen, joten suoran ![]() normaalin kulmakerroin on nolla.
normaalin kulmakerroin on nolla.
Kulmakerroin ![]() .
.
Kulmakertoimien tulon tulee olla ![]() , joten
, joten
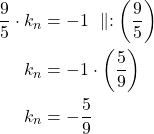
Suoran ![]() kulmakerroin on
kulmakerroin on ![]() . Ratkaistaan kulmakerroin, kun suoran ja normaalinen kulmakertoimien tulo on
. Ratkaistaan kulmakerroin, kun suoran ja normaalinen kulmakertoimien tulo on ![]() .
.
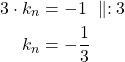
Normaalin kulmakerroin ![]() ja se kulkee pisteen
ja se kulkee pisteen ![]() kautta.
kautta.
Normaalin yhtälö on:
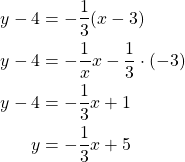
Suora ![]() on
on ![]() -akselin suuntainen suora, joten sen normaali on
-akselin suuntainen suora, joten sen normaali on ![]() -akselin suuntainen. Normaali kulkee pisteen
-akselin suuntainen. Normaali kulkee pisteen ![]() kautta, joten normaalin yhtälö on
kautta, joten normaalin yhtälö on ![]() .
.
Suora ![]() on
on ![]() -akselin suuntainen suora, joten sen normaali on
-akselin suuntainen suora, joten sen normaali on ![]() -akselin suuntainen, jolla ei siksi ole kulmakerrointa. Suora kulkee pisteen
-akselin suuntainen, jolla ei siksi ole kulmakerrointa. Suora kulkee pisteen ![]() kautta, joten normaalin yhtälö on
kautta, joten normaalin yhtälö on ![]() .
.
Pisteen ![]() etäisyys suorasta
etäisyys suorasta ![]() voidaan laskea kaavalla
voidaan laskea kaavalla
![]()
Suoran yhtälöstä saadaan kertoimet ![]() ,
, ![]() ja
ja ![]() .
.
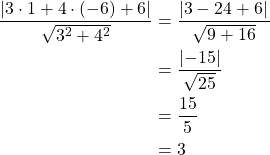
Pisteen ![]() etäisyys suorasta
etäisyys suorasta ![]() voidaan laskea kaavalla
voidaan laskea kaavalla
![]()
Suoran yhtälöstä saadaan kertoimet ![]() ,
, ![]() ja
ja ![]() .
.
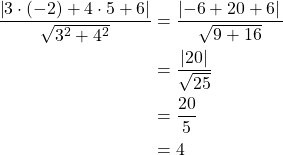
Pisteen ![]() etäisyys suorasta
etäisyys suorasta ![]() voidaan laskea kaavalla
voidaan laskea kaavalla
![]()
Suoran yhtälöstä saadaan kertoimet ![]() ,
, ![]() ja
ja ![]() .
.
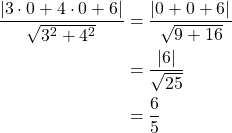
Kirjoitetaan suoran yhtälö normaalimuodossa
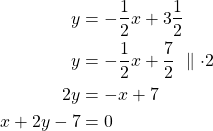
Pisteen ![]() etäisyys suorasta
etäisyys suorasta ![]() on
on
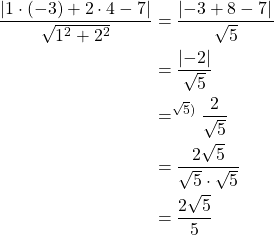
Kotitehtävät 375, 377, 378, 385, 387
Suora kulkee pisteen ![]() kautta ja se on
kautta ja se on ![]() -akselin suuntainen, joten
-akselin suuntainen, joten ![]() -koordinaatti on aina
-koordinaatti on aina ![]() . Suoran yhtälö on
. Suoran yhtälö on ![]() .
.
Suora kulkee pisteen ![]() kautta ja se on
kautta ja se on ![]() -akselin suuntainen, joten
-akselin suuntainen, joten ![]() -koordinaatti on aina
-koordinaatti on aina ![]() . Suoran yhtälö on
. Suoran yhtälö on ![]() .
.
Koska suoran suuntakulma ![]() , on suoran kulmakerroin
, on suoran kulmakerroin
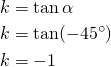
Määritetään suoran yhtälö, kun ![]() ja kulmakerroin
ja kulmakerroin ![]() . Suoran yhtälö saadaan lausekkeesta:
. Suoran yhtälö saadaan lausekkeesta:
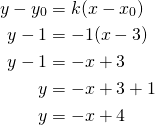
Määritetään ensin suoran ![]() kulmakerroin ratkaisemalla siitä
kulmakerroin ratkaisemalla siitä ![]() .
.
![]()
Kulmakerroin on siis ![]() . Suoran, joka on sitä vastaan kohtisuorassa, kulmakerroin on
. Suoran, joka on sitä vastaan kohtisuorassa, kulmakerroin on ![]() :n käänteisluvun vastaluku eli
:n käänteisluvun vastaluku eli ![]() . Tällöin kulmakertoimien tulo on
. Tällöin kulmakertoimien tulo on ![]() .
.
Huom! Jos ![]() , kohtisuorassa olevan suoran kulmakertoimen
, kohtisuorassa olevan suoran kulmakertoimen ![]() voi toki ratkaista yhtälöstä
voi toki ratkaista yhtälöstä
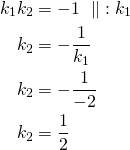
Suoran yhtälö saadaan lausekkeesta:
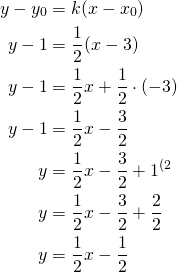
GeoGebralla on piirretty piste ![]() , suora
, suora ![]() ja suora
ja suora ![]() eli ratkaistussa muodossa
eli ratkaistussa muodossa ![]() .
.
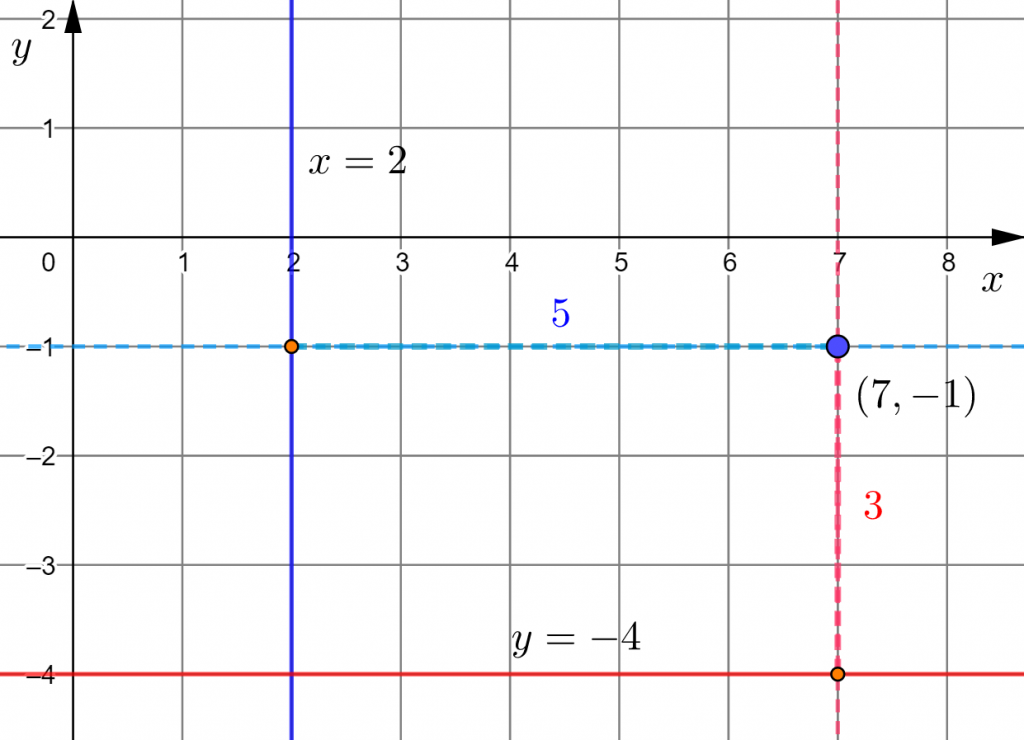
Kuvasta mittaamalla pisteen ![]() etäisyydeksi
etäisyydeksi
- suorasta
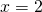 saadaan
saadaan 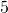
- suorasta
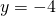 saadaan
saadaan 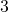 .
.
- Koska suora
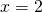 on pystysuora, pisteen
on pystysuora, pisteen 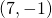 ja suoran etäisyys on
ja suoran etäisyys on 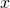 -koordinaattien erotus, eli
-koordinaattien erotus, eli 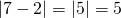 .
. - Koska suora
 on vaakasuora, pisteen etäisyys suorasta on
on vaakasuora, pisteen etäisyys suorasta on 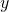 -koordinaattien erotus, eli
-koordinaattien erotus, eli 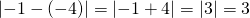 .
.
Kolmion ![]() ympäri piirretyn ympyrän keskipiste
ympäri piirretyn ympyrän keskipiste ![]() on janojen
on janojen ![]() ja
ja ![]()
(sekä ![]() ) keskinormaalien leikkauspiste.
) keskinormaalien leikkauspiste.
Määritetään ensin janan ![]() keskinormaali. Tätä varten tarvitaan
keskinormaali. Tätä varten tarvitaan
- janan
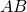 keskipiste ja
keskipiste ja - janan
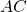 suuntaisen suoran kulmakerroin, jonka avulla määritetään
suuntaisen suoran kulmakerroin, jonka avulla määritetään - janan
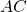 keskinormaalin kulmakerroin ja sen yhtälö.
keskinormaalin kulmakerroin ja sen yhtälö.
Janan ![]() keskipiste on
keskipiste on
![]()
Janan ![]() suuntaisen suoran kulmakerroin on
suuntaisen suoran kulmakerroin on
![]()
Siten keskinormaalin kulmakerroin on ![]() .
.
Muodostetaan janan ![]() keskinormaalin yhtälö lausekkeella
keskinormaalin yhtälö lausekkeella
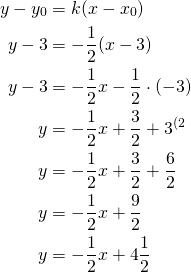
Määritetään samoin janan ![]() keskinormaali. Tätä varten tarvitaan
keskinormaali. Tätä varten tarvitaan
- janan
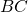 keskipiste ja
keskipiste ja - janan
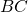 suuntaisen suoran kulmakerroin, jonka avulla määritetään
suuntaisen suoran kulmakerroin, jonka avulla määritetään - janan
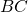 keskinormaalin kulmakerroin ja sen yhtälö.
keskinormaalin kulmakerroin ja sen yhtälö.
Janan ![]() keskipiste on
keskipiste on
![]()
Janan ![]() suuntaisen suoran kulmakerroin on
suuntaisen suoran kulmakerroin on
![]()
Siten keskinormaalin kulmakerroin on ![]() .
.
Muodostetaan janan ![]() keskinormaalin yhtälö lausekkeella
keskinormaalin yhtälö lausekkeella
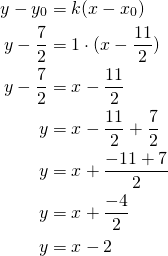
Lasketaan seuraavaksi keskinormaalien leikkauspiste, joka on kysytty ympyrän keskipiste ![]() .
.
Ratkaistaan yhtälöpari sijoitusmenetelmällä, koska molemmat suorat ovat ratkaistussa muodossa:
![Rendered by QuickLaTeX.com \[\begin{cases} y=-\frac{1}{2}x+4\frac{1}{2} \\y=x-2\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-62d4756365904f7d525f0cde41b34f41_l3.png)
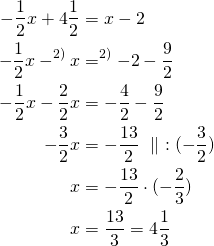
Sijoitetaan ![]() suoran
suoran ![]() yhtälöön, jolloin saadaan
yhtälöön, jolloin saadaan![]() .
.
Vastaus: Piste ![]()
Suorat ovat ![]() ja
ja ![]() .
.
Piirretään kuva GeoGebralla.
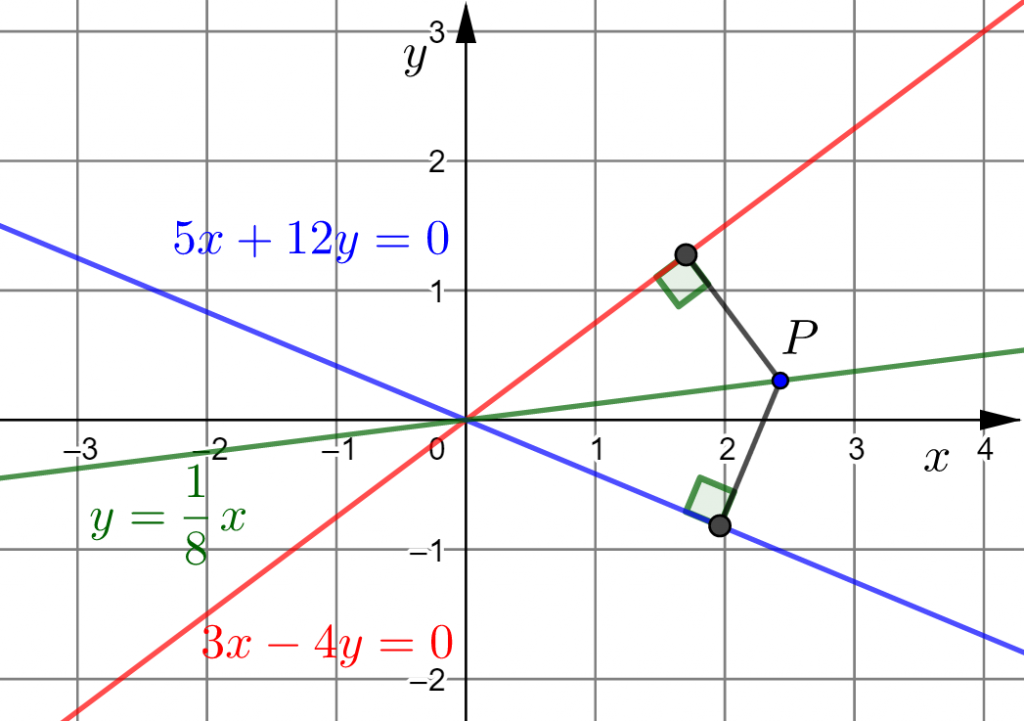
Piste ![]() on kulman puolittajalla, jos se on yhtä kaukana kulman kyljistä.
on kulman puolittajalla, jos se on yhtä kaukana kulman kyljistä.
Lasketaan pisteen ![]() etäisyys
etäisyys
- suorasta
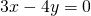 ja
ja - suorasta
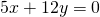
Suoran normaalimuotoisen yhtälön yleinen lauseke on
![]()
Pisteen ![]() etäisyys suorasta lasketaan lausekkeella
etäisyys suorasta lasketaan lausekkeella
![]()
Kun tiedetään pisteen ![]() -koordinaatit, niin ne sijoitetaan tavallisesti
-koordinaatit, niin ne sijoitetaan tavallisesti ![]() :n paikalle, mutta nyt selvitetään, mikä on piste
:n paikalle, mutta nyt selvitetään, mikä on piste ![]() .
.
Lasketaan pisteen ![]() etäisyys suorasta
etäisyys suorasta ![]() . Tällöin
. Tällöin
![Rendered by QuickLaTeX.com \[\begin{cases}a=3\\b=-4\\c=0\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-106f63894ee8935b8b4a9b0e5fe850b4_l3.png)
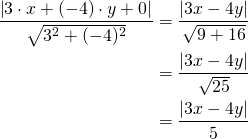
Lasketaan pisteen ![]() etäisyys suorasta
etäisyys suorasta ![]() . Tällöin
. Tällöin
![Rendered by QuickLaTeX.com \[\begin{cases}a=5\\b=12\\c=0\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-f09fdd6d7f18676bdf81f022129f2311_l3.png)
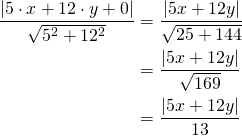
Koske pisteen ![]() etäisyyden molemmista suorista pitää olla sama, saadaan yhtälö
etäisyyden molemmista suorista pitää olla sama, saadaan yhtälö
![]()
Ratkaistaan yhtälöstä muuttuja ![]() .
.
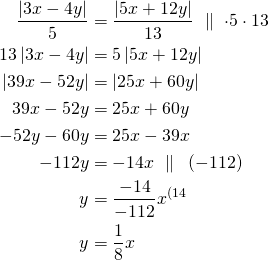
tai
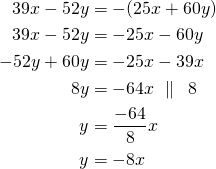
Suoran ![]() kulmakerroin saadaan, kun ratkaistaan
kulmakerroin saadaan, kun ratkaistaan ![]() . Samoin saadaan suoran
. Samoin saadaan suoran ![]() kulmakerroin
kulmakerroin ![]() .
.
Koska kulmanpuolittaja on suorien ![]() ja
ja ![]() välissä, sen kulmakertoimen tulee olla välillä
välissä, sen kulmakertoimen tulee olla välillä ![]() .
.
Tämän perusteella valitaan se kulmanpuolittaja, jonka kulmakerroin on ![]() .
.
Vastaus: Suora on ![]() .
.
Kysytyn pistejoukon muodostavat kaksi suoran ![]() kanssa yhdensuuntaista suoraa. Piirretään GeoGebralla suora
kanssa yhdensuuntaista suoraa. Piirretään GeoGebralla suora ![]() sekä siitä etäisyydellä
sekä siitä etäisyydellä ![]() olevat yhdensuuntaiset suorat.
olevat yhdensuuntaiset suorat.
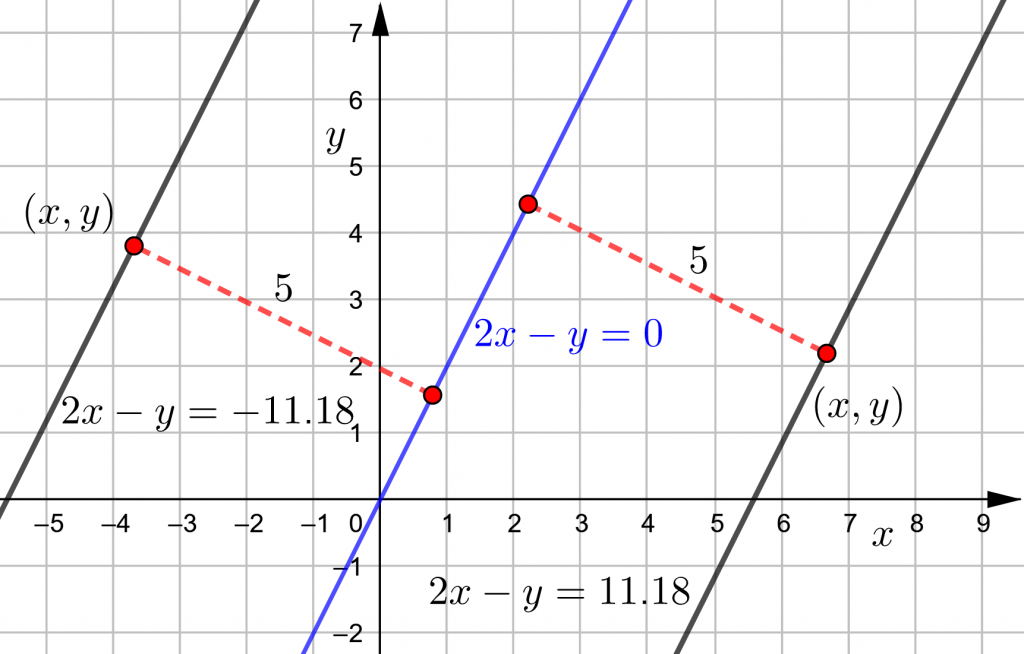
Merkitään pistejoukon pistettä ![]() . Sen etäisyys suorasta
. Sen etäisyys suorasta ![]() on viisi. Saadaan yhtälö
on viisi. Saadaan yhtälö
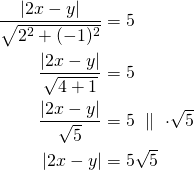
Tästä voidaan ratkaista
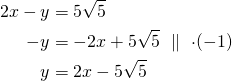
tai