Tehtävien ratkaisut
Tuntitehtävät
- Luku 3.1 Suoran suunta: 301, 303a, 305, 309, 313.
- Luku 3.2 Suoran yhtälö: 321, 326, 327a, 330, 331, 332, 340.
Suora ![]() , pisteet
, pisteet ![]() ja
ja ![]() .
.
Kulmakerroin ![]()
Suora ![]() , pisteet
, pisteet ![]() ja
ja ![]() .
.
Kulmakerroin ![]()
Suora ![]() , pisteet
, pisteet ![]() ja
ja ![]() .
.
Kulmakerroin ![]()
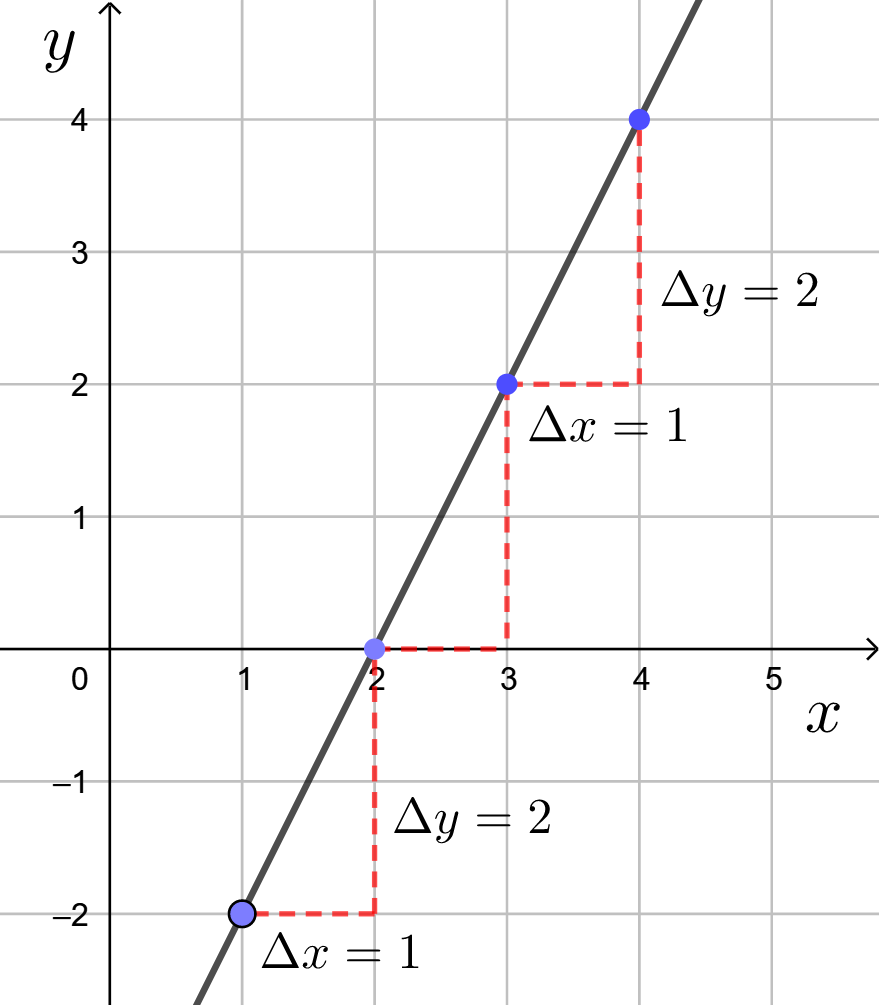
Suora kulkee pisteen ![]() kautta ja kulmakerroin on
kautta ja kulmakerroin on ![]() . Kun
. Kun ![]() -koordinaatti muuttuu oikealle yhden yksikön verran,
-koordinaatti muuttuu oikealle yhden yksikön verran, ![]() -koordinaatti muuttuu ylös kahden yksikön verran.
-koordinaatti muuttuu ylös kahden yksikön verran.
Siten toinen ![]() -koordinaatti on esimerkiksi
-koordinaatti on esimerkiksi ![]() ja
ja ![]() -koordinaatti on esimerkiksi
-koordinaatti on esimerkiksi ![]() eli koordinaatitksi tulee
eli koordinaatitksi tulee ![]() .
.
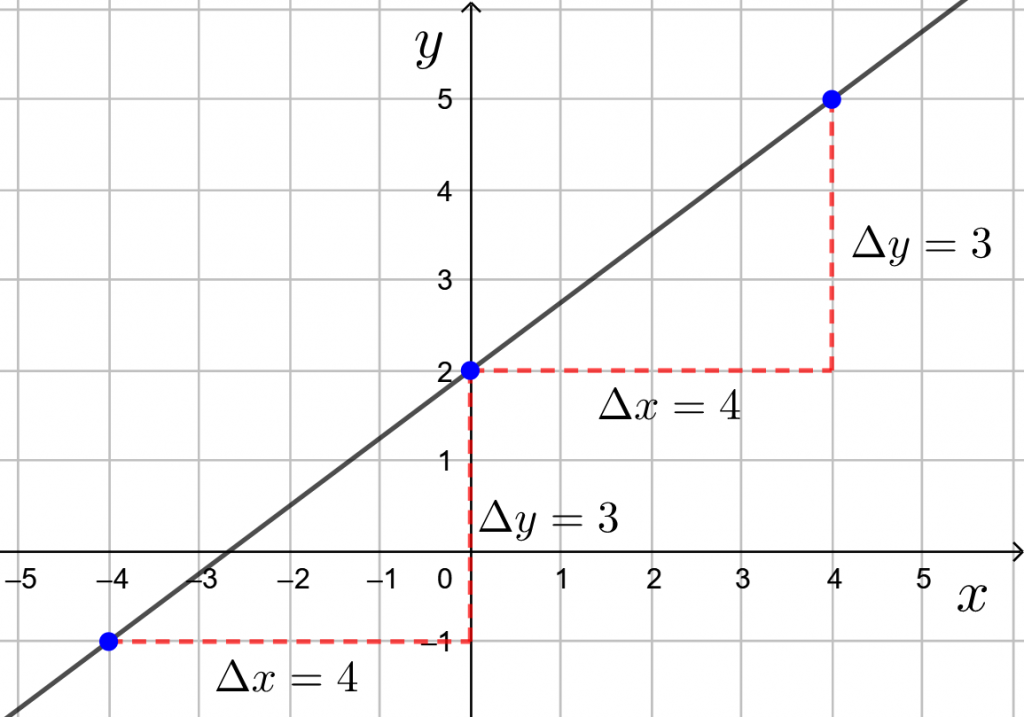
Suora kulkee pisteen ![]() kautta ja kulmakerroin on
kautta ja kulmakerroin on ![]() . Kun
. Kun ![]() -koordinaatti muuttuu oikealle neljän yksikön verran,
-koordinaatti muuttuu oikealle neljän yksikön verran, ![]() -koordinaatti muuttuu ylös kolmen yksikön verran.
-koordinaatti muuttuu ylös kolmen yksikön verran.
Siten toinen ![]() -koordinaatti on esimerkiksi
-koordinaatti on esimerkiksi ![]() ja
ja ![]() -koordinaatti on esimerkiksi
-koordinaatti on esimerkiksi ![]() eli koordinaatitksi tulee
eli koordinaatitksi tulee ![]() .
.
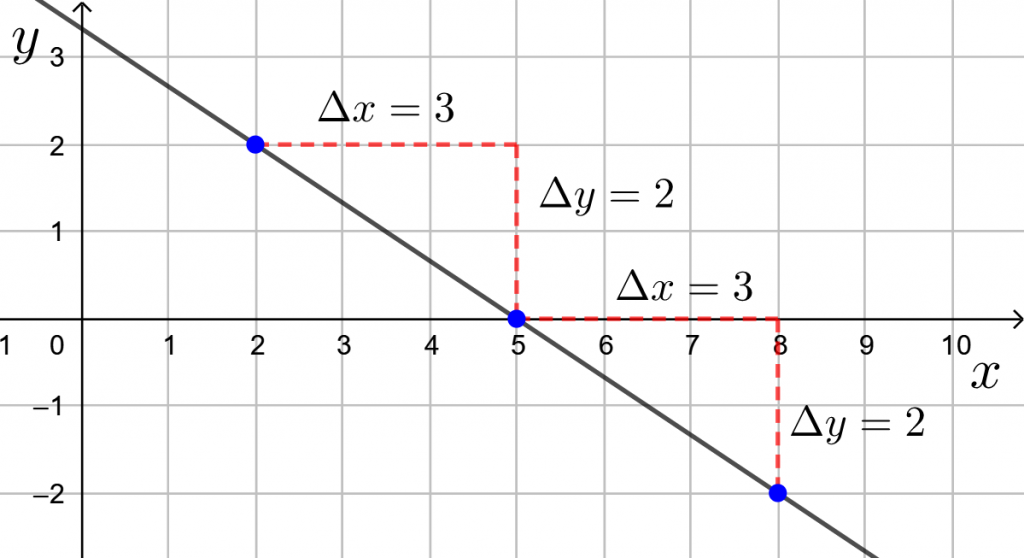
Suora kulkee pisteen ![]() kautta ja kulmakerroin on
kautta ja kulmakerroin on ![]() . Kun
. Kun ![]() -koordinaatti muuttuu oikealle kolmen yksikön verran,
-koordinaatti muuttuu oikealle kolmen yksikön verran, ![]() -koordinaatti muuttuu alas kahden yksikön verran.
-koordinaatti muuttuu alas kahden yksikön verran.
Siten toinen ![]() -koordinaatti on esimerkiksi
-koordinaatti on esimerkiksi ![]() ja
ja ![]() -koordinaatti on esimerkiksi
-koordinaatti on esimerkiksi ![]() eli koordinaatitksi tulee
eli koordinaatitksi tulee ![]() .
.
Suoran kulmakerroin on ![]() . Siten
. Siten ![]() .
.
Suoran suuntakulma on
![]()
Huom! Voit kirjoittaa jatkossa suoraan seuraavasti:
![]()
Lasketaan ensin suoran kulmakerroin. Pisteet ovat ![]() ja
ja ![]() .
.
![]()
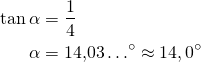
Suora kulkee pisteiden ![]() ja
ja ![]() kautta. Suoran pisteillä on sama
kautta. Suoran pisteillä on sama ![]() -koordinaatti. Suora on siten pystysuora. Sen suuntakulma on
-koordinaatti. Suora on siten pystysuora. Sen suuntakulma on ![]() .
.
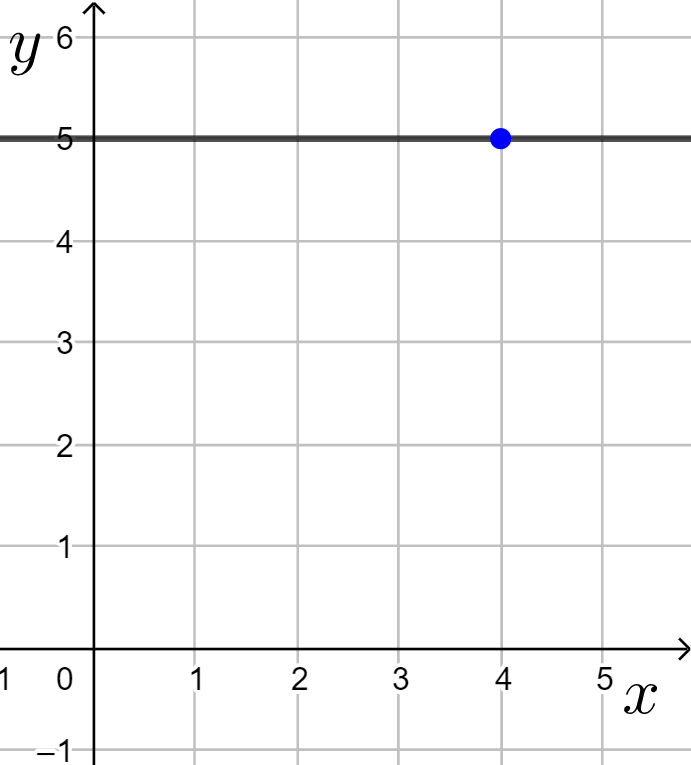
Suoran eräs suuntavektori ![]() tarkoittaa sitä, että suora on
tarkoittaa sitä, että suora on ![]() -akselin suuntainen eli se on vaakasuora. Suuntakulma on
-akselin suuntainen eli se on vaakasuora. Suuntakulma on ![]() .
.
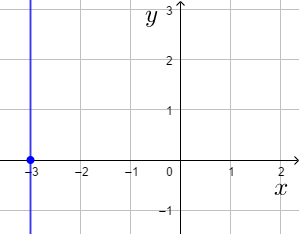
Suora leikkaa ![]() -akselin pisteessä
-akselin pisteessä ![]() ja on
ja on ![]() -akselin suuntainen tarkoittaa pystysuoraa suoraa.
-akselin suuntainen tarkoittaa pystysuoraa suoraa.
Tällainen suuntavektori on esimerkiksi ![]() tai
tai ![]() .
.
Suoran suuntavektori voidaan määrittää laskemalla pisteiden ![]() ja
ja ![]()
![]() -, ja
-, ja ![]() -koordinaattien erotukset:
-koordinaattien erotukset:
![]()
Kun kulmakerroin on ![]() , suora on
, suora on ![]() -akselin suuntainen. Suoran eräs suuntavektori on
-akselin suuntainen. Suoran eräs suuntavektori on ![]() .
.
Kulmakerroin ![]() .
.
Kulmakerroin ![]() .
.
Yleensä vastaukseen ei jätetä neliöjuurta nimittäjään. Lavennetaan ![]() :lla.
:lla.
![]()
![]() , piste
, piste ![]()
Sijoitetaan suoran yhtälön lausekkeeseen, jolloin
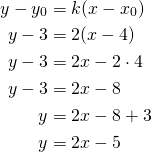
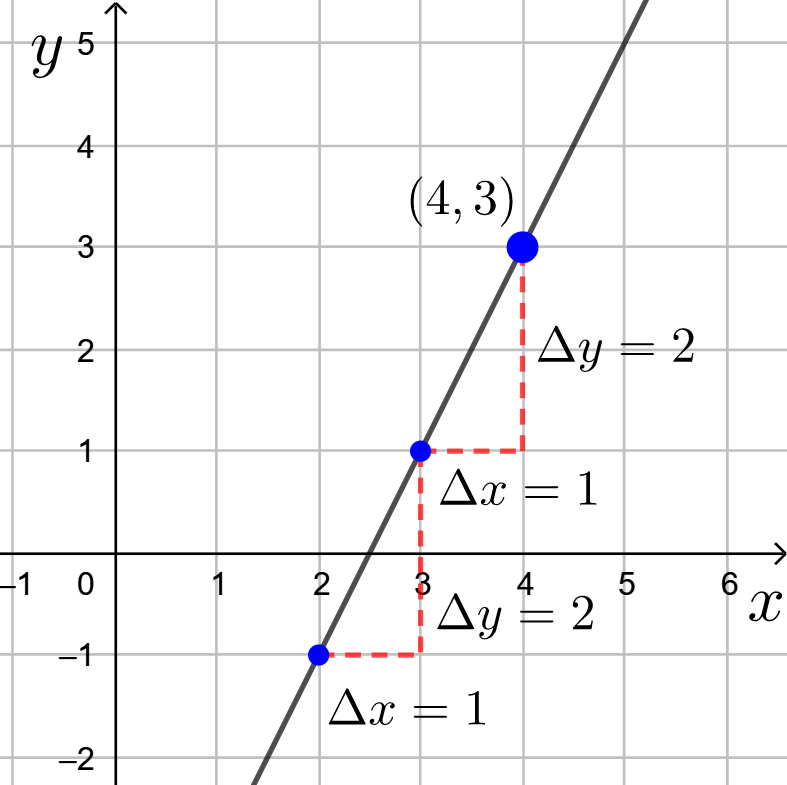
Piste on suoralla, jos se toteuttaa suoran yhtälön. Sijoitetaan suoran yhtälöön ![]() pisteen koordinaatit.
pisteen koordinaatit.
Piste ![]() :
:
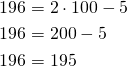
Piste ei toteuta yhtälöä, joten se ei ole suoralla.
Piste ![]() :
:
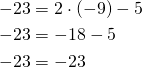
Piste toteuttaa yhtälön, joten se on suoralla.
Ratkaistaan normaalimuodossa olevista yhtälöistä muuttuja ![]() .
.
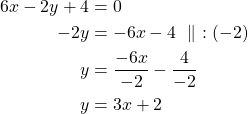
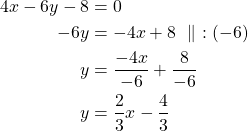
Ensimmäisen suoran kulmakerroin on ![]() ja toisen suoran kulmakerroin on
ja toisen suoran kulmakerroin on ![]() . Koska kulmakertoimien arvot eivät ole yhtäsuuret, suorat eivät ole yhdensuuntaisia.
. Koska kulmakertoimien arvot eivät ole yhtäsuuret, suorat eivät ole yhdensuuntaisia.
Siirretään kaikki termit samalle puolelle yhtälöä ja lavennetaan tarvittaessa murtolukukertoimet kokonaisluvuiksi.
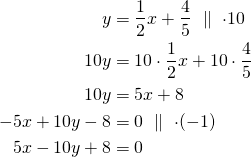
Ratkaistaan normaalimuotoisesta yhtälöstä ![]() :
:
![]()
Suoran kulmakerroin on ![]() . Suora leikkaa
. Suora leikkaa ![]() -akselin pisteessä
-akselin pisteessä ![]() .
.
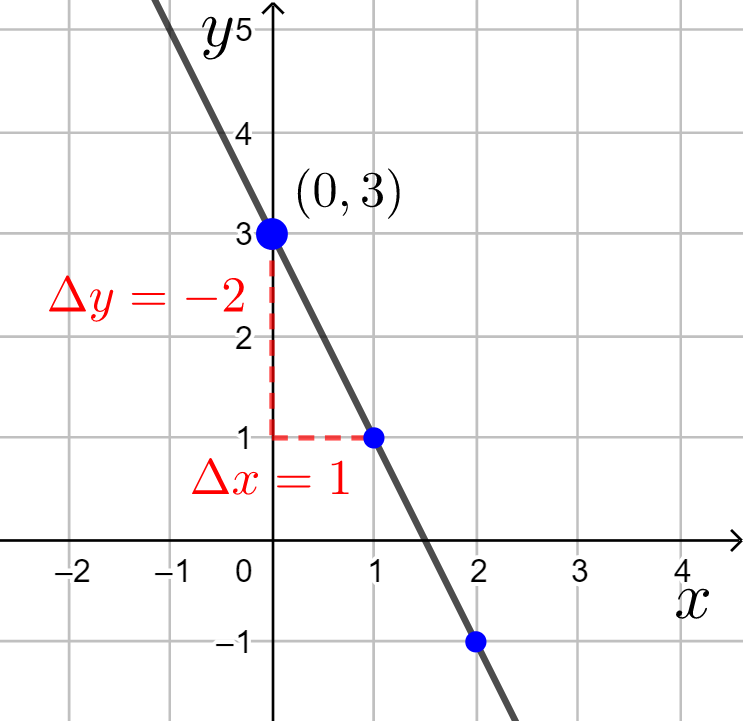
Suuntakulman selvittämiseksi ratkaistaan yhtälön normaalimuodosta ![]() :
:
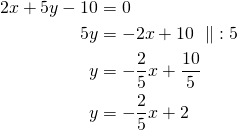
Kulmakerroin on ![]()
Suuntakulma ![]() määritetään kulmakertoimen avulla
määritetään kulmakertoimen avulla
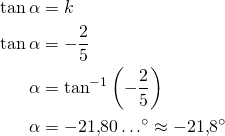
Kirjoitetaan oleva yhtälö ratkaistuun muotoon:
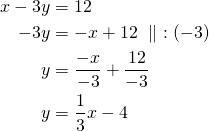
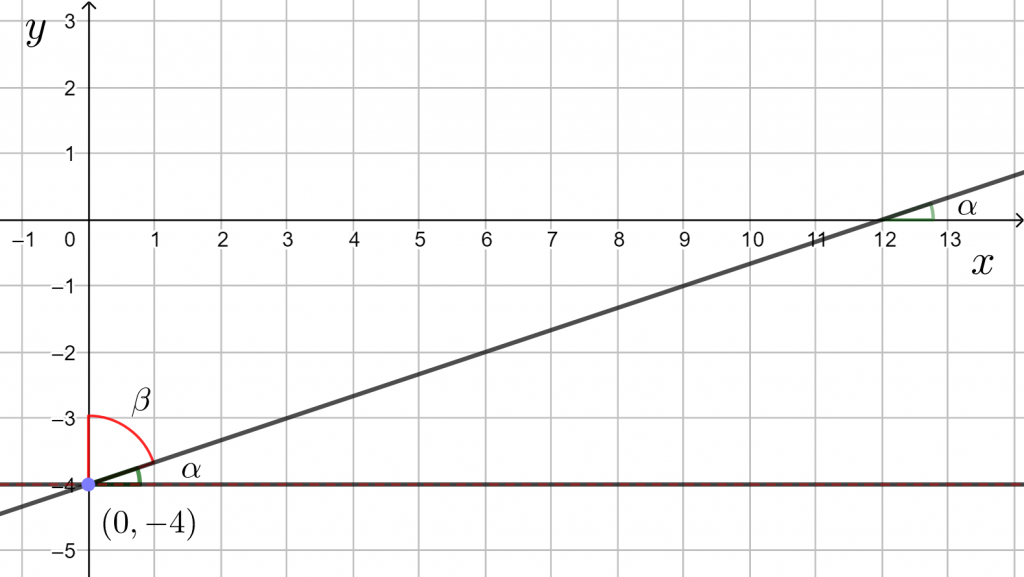
Suoran kulmakerroin ![]() .
.
Suuntakulma ![]() on
on
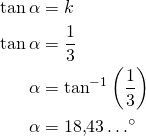
Suora leikkaa ![]() -akselin kuvaan merkityssä kulmassa
-akselin kuvaan merkityssä kulmassa ![]() . Koska suuntakulma tarkoittaa suoran ja
. Koska suuntakulma tarkoittaa suoran ja ![]() -akselin välistä kulmaa, ja koska koordinaattiakseleiden välillä on suorakulma eli
-akselin välistä kulmaa, ja koska koordinaattiakseleiden välillä on suorakulma eli ![]() , saadaan kysyksi kulmaksi
, saadaan kysyksi kulmaksi
![]()
Lasketaan suoran ![]() ja
ja ![]() -akselin leikkauspiste. Siinä
-akselin leikkauspiste. Siinä ![]() -koordinaatti on
-koordinaatti on ![]() . Sijoitetaan
. Sijoitetaan ![]() :n paikalle
:n paikalle ![]() ja ratkaistaan
ja ratkaistaan ![]() :
:
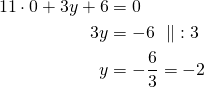
Suora ![]() leikkaa
leikkaa ![]() -akselin pisteessä
-akselin pisteessä ![]() .
.
Koska suora ![]() on yhdensuuntainen suoran
on yhdensuuntainen suoran ![]() kanssa, niillä on yhtä suuri kulmakerroin. Ratkaistaan suoran
kanssa, niillä on yhtä suuri kulmakerroin. Ratkaistaan suoran ![]() kulmakerroin:
kulmakerroin:
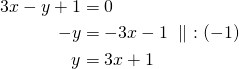
Suoran ![]() kulmakerroin on siis
kulmakerroin on siis ![]() ja suora kulkee pisteen
ja suora kulkee pisteen ![]() kautta. Määritetään suoran yhtälö:
kautta. Määritetään suoran yhtälö:
![]()
Huom! Suoran yhtälön voi määrittää myös sijoittamalla kulmakertoimen arvon ja pisteen ![]() koordinaatit suoran yhtälön lausekkeeseen
koordinaatit suoran yhtälön lausekkeeseen
![]()
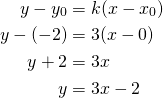
Vastaus: Suoran yhtälö on ![]() .
.
Kun suora leikkaa ![]() -akselin,
-akselin, ![]() -koordinaatti on
-koordinaatti on ![]() .
.
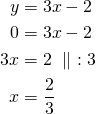
Vastaus: Suora leikkaa ![]() -akselin pisteessä
-akselin pisteessä ![]() .
.
Suora kulkee pisteen ![]() kautta, jos piste toteuttaa suoran yhtälön.
kautta, jos piste toteuttaa suoran yhtälön.
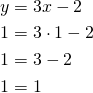
Piste toteuttaa suoran yhtälön, joten se on suoralla.
Kotitehtävät
- Luku 3.1 Suoran suunta: 302, 314, 319.
- Luku 3.2 Suoran yhtälö: 322, 327bcd, 332, 340.
![]()
![]()
![]()
Koska nimittäjä on ![]() , suoralla ei ole kulmakerrointa.
, suoralla ei ole kulmakerrointa.
Suora kulkee pisteiden ![]() ja
ja ![]() kautta, joten sen kulmakerroin on
kautta, joten sen kulmakerroin on
![]()
Jos jokin piste ![]() ,
, ![]() tai
tai ![]() on suoralla, täytyy pisteestä
on suoralla, täytyy pisteestä ![]() pisteisiin
pisteisiin ![]() ,
, ![]() ja
ja ![]() kulkevien suorien kulmakertoimien olla samoin
kulkevien suorien kulmakertoimien olla samoin ![]() . Lasketaan kulmakertoimet.
. Lasketaan kulmakertoimet.
Pisteet ![]() ja
ja ![]()
![]()
Koska ![]() , piste
, piste ![]() ei ole suoralla.
ei ole suoralla.
Pisteet ![]() ja
ja ![]()
![]()
Koska ![]() , piste
, piste ![]() ei ole suoralla.
ei ole suoralla.
Pisteet ![]() ja
ja ![]()
![]()
Koska ![]() , piste
, piste ![]() on suoralla.
on suoralla.
Suuntavektorin ![]() suuntaisen suoran kulmakerroin
suuntaisen suoran kulmakerroin
![]() . Suorat eivät ole yhdensuuntaiset.
. Suorat eivät ole yhdensuuntaiset.
Kulmakerroin ![]() . Suorat ovat yhdensuuntaiset.
. Suorat ovat yhdensuuntaiset.
Suuntavektorin ![]() suuntaisen suoran kulmakerroin
suuntaisen suoran kulmakerroin
![]()
![]()
Suorat ovat yhdensuuntaiset.
Piste ![]() on funktion
on funktion ![]() kuvaajalla, joten pisteen
kuvaajalla, joten pisteen ![]()
![]() -koordinaatti on
-koordinaatti on ![]() .
.
Piste ![]() on siten
on siten ![]() .
.
Origon ![]() ja pisteen
ja pisteen ![]() kautta kulkevan suoran kulmakerroin on
kautta kulkevan suoran kulmakerroin on
![]()
Tämän kulmakertoimen tulee olla ![]() . Saadaan siis yhtälö, josta ratkaistaan
. Saadaan siis yhtälö, josta ratkaistaan ![]() .
.
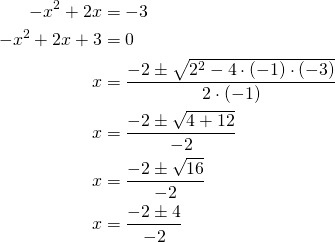
Saadaan
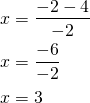
tai
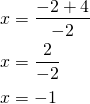
Lasketaan ![]() :n arvot:
:n arvot:
Kun ![]() ,
, ![]() .
.
Kun ![]() ,
, ![]() .
.
Vastaus: Kulmakerroin on ![]() , kun piste
, kun piste ![]() tai
tai ![]() .
.
Kulmakerroin on positiivinen, kun ![]() .
.
Lausekkeen ![]() kuvaaja on alaspäin aukeava paraabeli.
kuvaaja on alaspäin aukeava paraabeli.
Ratkaistaan nollakohdat.
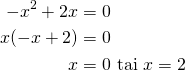
Lausekkeen kuvaaja on alaspäin aukeneva paraabeli, jolla on kaksi nollakohtaa.
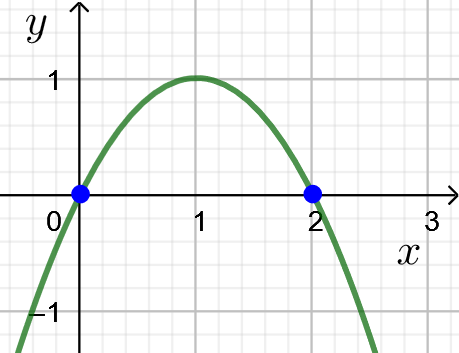
Arvot ovat positiivisia eli ![]() , kun
, kun ![]() .
.
Kulmakertoimen lauseke ![]() saa suurimman arvonsa paraabelin huipussa, joka on nollakohtien puolivälissä, kohdassa
saa suurimman arvonsa paraabelin huipussa, joka on nollakohtien puolivälissä, kohdassa ![]() .
.
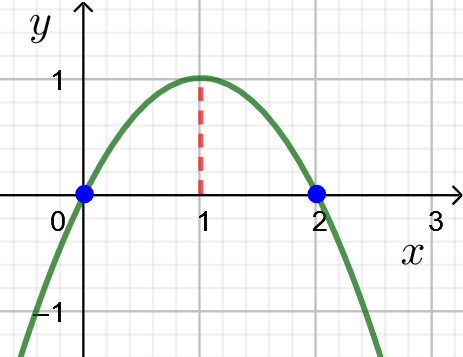
Tällöin ![]() -koordinaatti on
-koordinaatti on ![]() .
.
Piste ![]() .
.
Suora kulkee pisteen ![]() kautta.
kautta.
Koska suora on ![]() -akselin suuntainen, sen kulmakerroin
-akselin suuntainen, sen kulmakerroin ![]() on nolla.
on nolla.
Suoran yhtälö ![]() .
.
Tämän voi myös kirjoittaa suoran yhtälön lausekkeella:
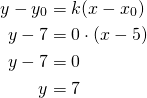
Koska suora on ![]() -akselin suuntainen, sillä ei ole kulmakerrointa.
-akselin suuntainen, sillä ei ole kulmakerrointa.
Suoran yhtälö on siten ![]() .
.
Suoran yhtälö normaalimuodossa on ![]() .
.
Kirjoitetaan suoran yhtälö ratkaistussa muodossa.
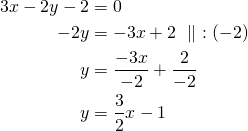
Tästä muodosta nähdään, että suoran kulmakerroin on ![]() . Suoran ja
. Suoran ja ![]() -akselin leikkauspiste on kohdassa
-akselin leikkauspiste on kohdassa ![]() .
.
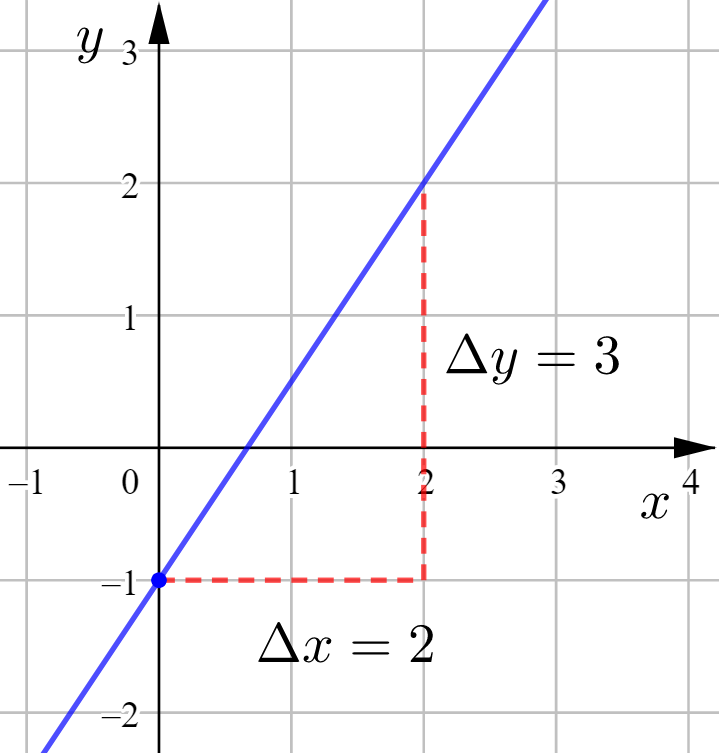
Suora on pystysuora ![]() .
.
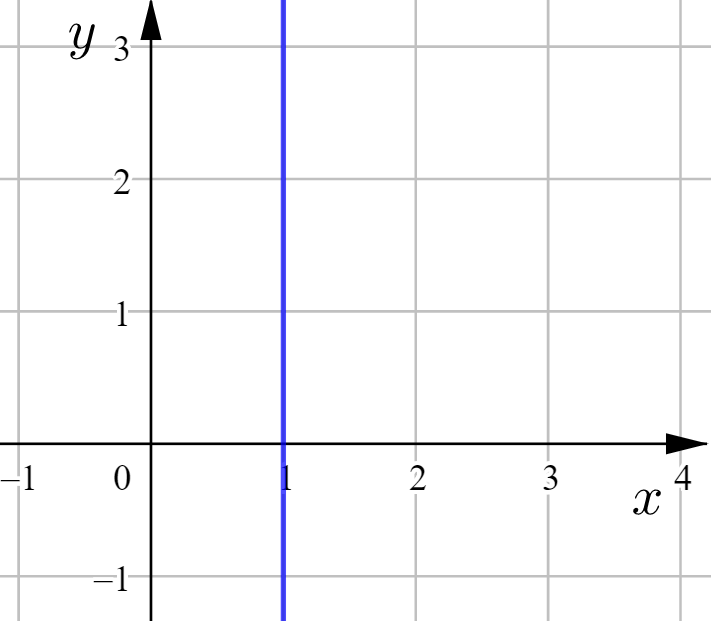
Suora ![]() on ratkaistussa muodossa
on ratkaistussa muodossa ![]() . Suora on vaakasuora ja leikkaa
. Suora on vaakasuora ja leikkaa ![]() -akselin kohdassa
-akselin kohdassa ![]() .
.
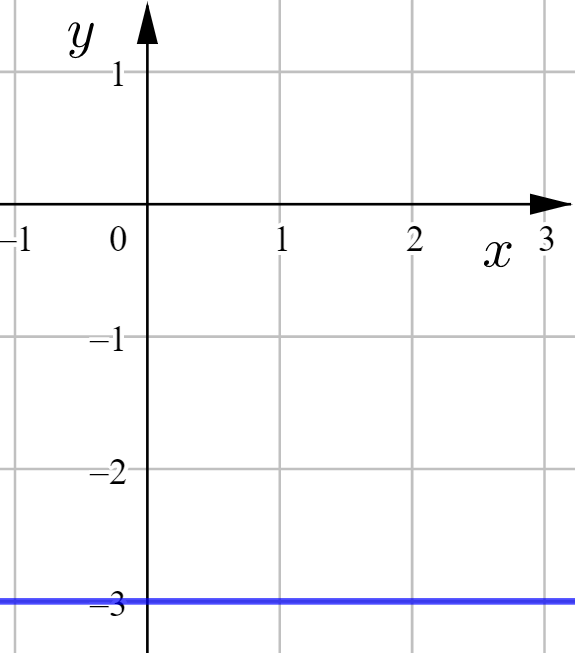
Saadaan yhtälö ![]() , joka ratkaistussa muodossa on
, joka ratkaistussa muodossa on ![]() .
.
Tämän suoran kulmakerroin on ![]() , ja se leikkaa
, ja se leikkaa ![]() -akselin pisteessä
-akselin pisteessä ![]() .
.
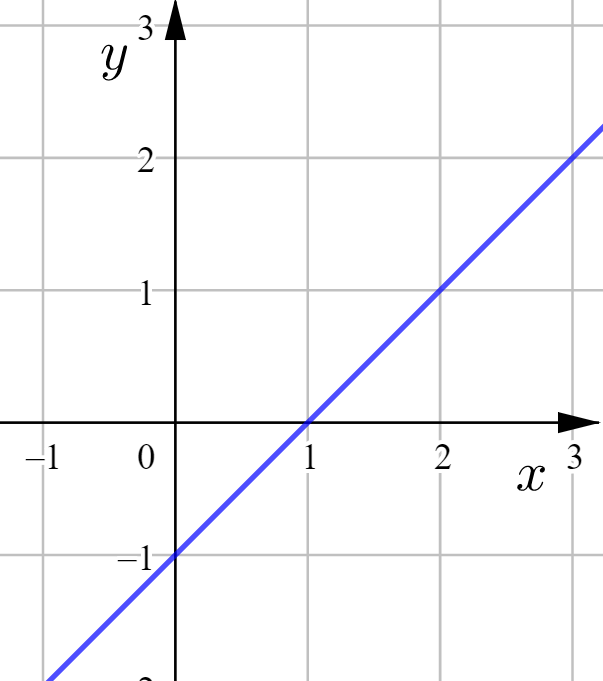
Suoran yhtälö on ![]()
Ratkaistaan ![]() :
:
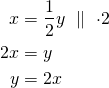
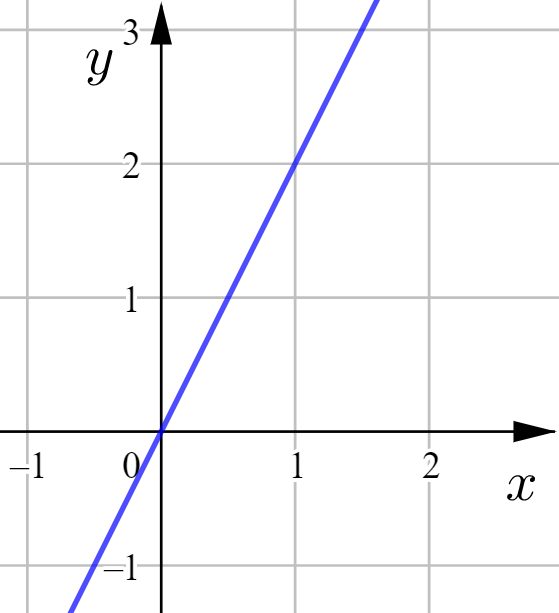
Tämän suoran kulmakerroin on ![]() , ja se leikkaa
, ja se leikkaa ![]() -akselin origossa.
-akselin origossa.
Suoran yhtälö on ![]() . Ratkaistaan
. Ratkaistaan ![]() .
.
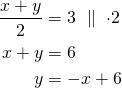
Tämän suoran kulmakerroin on ![]() , ja se leikkaa
, ja se leikkaa ![]() -akselin pisteessä
-akselin pisteessä ![]() .
.
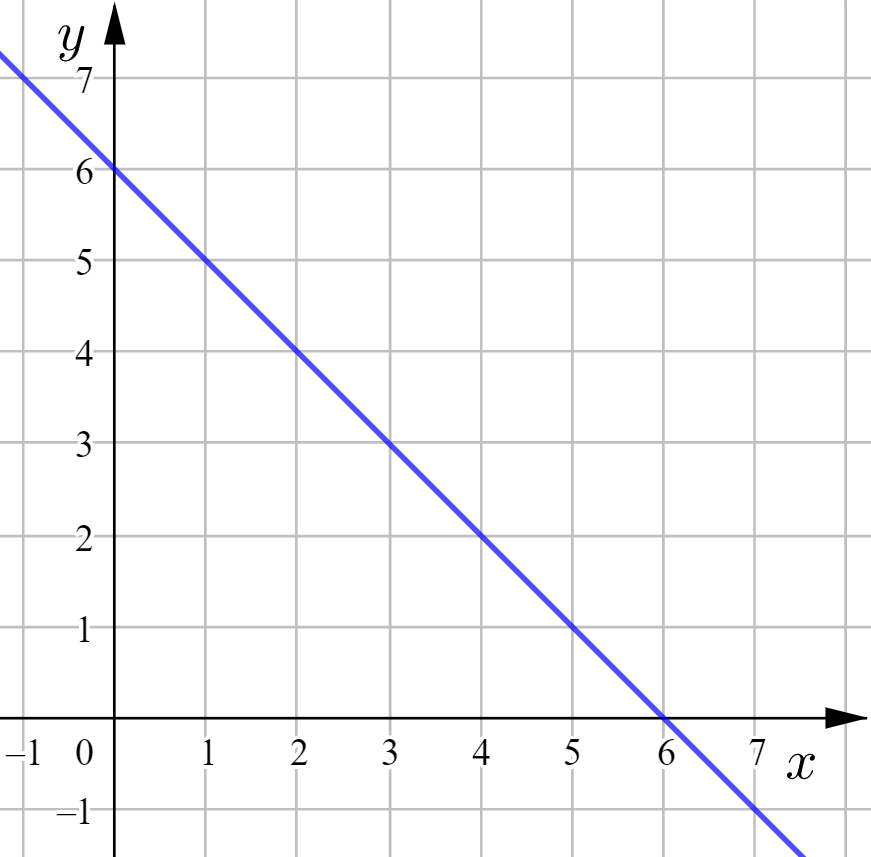
Suora ![]() leikkaa
leikkaa ![]() -akselin pisteessä
-akselin pisteessä ![]() .
.
Ratkaistaan ![]() -akselin leikkauskohta.
-akselin leikkauskohta. ![]() -akselilla
-akselilla ![]() .
.
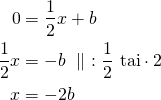
Suora leikkaa ![]() -akselin pisteessä
-akselin pisteessä ![]() .
.
Suoran ![]() kulmakerroin on
kulmakerroin on ![]() . Leikkauspisteen koordinaatit voivat olla positiivisia tai negatiivisia.
. Leikkauspisteen koordinaatit voivat olla positiivisia tai negatiivisia.
Hahmotellaan kuva.
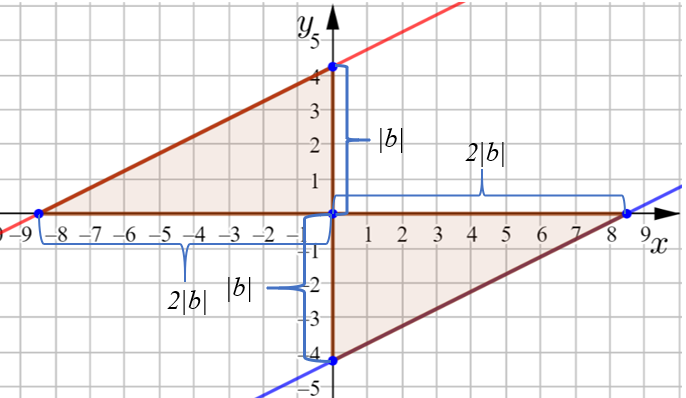
Jos vakio ![]() on positiivinen, ylempi suoran on kyseessä. Jos
on positiivinen, ylempi suoran on kyseessä. Jos ![]() on negatiivinen, kyseessä on alempi suora.
on negatiivinen, kyseessä on alempi suora.
Suoran ja ![]() -akselin leikkauspisteen etäisyys origosta on
-akselin leikkauspisteen etäisyys origosta on ![]() .
.
Suoran ja ![]() -akselin leikkauspisteen etäisyys origosta on
-akselin leikkauspisteen etäisyys origosta on ![]() .
.
Suoran ja koordinaattiakseleiden rajaaman kolmion pinta-ala on 18. Muodostetaan pinta-alan lauseke seuraavasti:
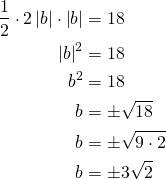
Vastaus: ![]() tai
tai ![]() .
.