Tällä sivulla on
- Tuntimuistiinpanot luvuista 2.2 ja 3.1 torstaina 26.8.2021
- Luku 2.2: Tehtävien 225b, 226, 227, 228, 229, 230, 232, 237 ratkaisut.
- Luku 3.1: Tehtävien 301, 302, 303 ratkaisut.
Piirretään käyrien ![]() ja
ja ![]() kuvaajat GeoGebralla.
kuvaajat GeoGebralla.

Kuvaajat näyttäisivät leikkaavan pisteissä ![]() ja
ja ![]() .
.
Tarkistetaan laskemalla sijoittamalla pisteiden koordinaatit yhtälöihin ![]() ja
ja ![]() . Lasketaan yhtälöiden vasemmat puolet. Piste on leikkauspiste, jos se toteuttaa molemmat yhtälöt.
. Lasketaan yhtälöiden vasemmat puolet. Piste on leikkauspiste, jos se toteuttaa molemmat yhtälöt.
Piste ![]() :
:
![Rendered by QuickLaTeX.com \[\begin{cases}3^2+4^2&=25\\2 \cdot 3^2 -3 \cdot 4&=6\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-b92c27c25ed47899230da855beaca96d_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases}9+16&=25\\2 \cdot 9 -12&=6\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-b4747f48cbe5c0ed7d82bb45e1606355_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases}25&=25\\28 -12&=6\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-d7fa67c1126c9ec85737ec8755542430_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases}25&=25\\6&=6\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-340e1de385879837edbef0bc5d76e4e5_l3.png)
Siten piste ![]() toteuttaa yhtälöparin.
toteuttaa yhtälöparin.
Piste ![]() :
:
![Rendered by QuickLaTeX.com \[\begin{cases}(-3)^2+4^2&=25\\2 \cdot (-3)^2 -3 \cdot 4&=6\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-bb7a6610c0a11146983526a18112c577_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases}9+16&=25\\2 \cdot 9 -12&=6\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-b4747f48cbe5c0ed7d82bb45e1606355_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases}25&=25\\28 -12&=6\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-d7fa67c1126c9ec85737ec8755542430_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases}25&=25\\6&=6\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-340e1de385879837edbef0bc5d76e4e5_l3.png)
Siten piste ![]() toteuttaa yhtälöparin.
toteuttaa yhtälöparin.
Yhtälöparin ratkaisut ovat siis
![Rendered by QuickLaTeX.com \[\begin{cases}y&=4\\y&=3\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-a55d026eeb272b17272a4251f098d83c_l3.png)
ja
![Rendered by QuickLaTeX.com \[\begin{cases}x=24\\y=-3\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-eaf5a78f8ff9d0db0a920cdc6e3ffff2_l3.png)
Käyrän yhtälö on ![]() .
.
Kun käyrä leikkaa ![]() -akselin, jolloin
-akselin, jolloin ![]() -koordinaatti on nolla. Sijoitetaan käyrän yhtälössä
-koordinaatti on nolla. Sijoitetaan käyrän yhtälössä ![]() :n paikalle
:n paikalle ![]() . Saadaan yhtälö
. Saadaan yhtälö
![]()
Ratkaistaan toisen asteen yhtälö GeoGebralla:

Vastaus: Käyrä leikkaa ![]() -akselin pisteissä
-akselin pisteissä ![]() ja
ja ![]() .
.
Lasketaan käyrän ja suoran ![]() leikkauspisteet: Sijoitetaan
leikkauspisteet: Sijoitetaan ![]() :n paikalle
:n paikalle ![]() ja ratkaistaan
ja ratkaistaan ![]() .
.

Ratkaistaan toisen asteen yhtälö GeoGebralla. Nyt muuttujana on ![]() .
.

Vastaus: Käyrä leikkaa käyrän ![]() -akselin pisteissä
-akselin pisteissä ![]() ja
ja ![]() .
.
Piirretään käyrä ![]() ja käyrä
ja käyrä ![]()
Valitse Leikkauspisteet.
Klikkaa sitten vuoronperään kumpaakin käyrää.


Yllä olevaan kuvaan olen muokannut leikkauspisteiden väriä, poistanut nimet, poistanut käyrien nimet (eq1, jne.)
Piste ![]() .
.
Määritetään käyrien yhtälöt
Pisteiden ![]() -koordinaatti on
-koordinaatti on ![]() -koordinaatin ja luvun
-koordinaatin ja luvun ![]() erotuksen neliö tarkoittaa käyrää
erotuksen neliö tarkoittaa käyrää
![]()
Pisteiden ![]() – ja
– ja ![]() -koordinaattien neliöiden summa on
-koordinaattien neliöiden summa on ![]() tarkoittaa käyrää
tarkoittaa käyrää
![]()
Piste on käyrällä, jos se toteuttaa käyrän yhtälön. Sijoitetaan kummankin käyrän yhtälöön pisteen ![]() koordinaatit.
koordinaatit.

Siten piste on käyrällä ![]() .
.

Siten piste on käyrällä ![]() .
.
Piirretään kuva GeoGebralla.

Katso sama videolta:
Ratkaisu GeoGebralla:
![]() .
.
Piirretään samaan koodrinaatistoon käyrät ![]() ja
ja ![]() .
.

Koska käyrät leikkaavat pisteissä ![]() ja
ja ![]() , niin yhtälön
, niin yhtälön ![]() ratkaisuja ovat
ratkaisuja ovat ![]() ja
ja ![]() .
.
Ratkaistaan itseisarvoyhtälö ![]() algebrallisesti.
algebrallisesti.
Saadaan kaksi yhtälöä

tai

Vastaus: Itseisarvoyhtälön ratkaisut ovat ![]() tai
tai ![]() .
.
Ratkaistaan itseisarvoyhtälö ![]() GeoGebralla. Piirretään samaan koordinaatistoon käyrät
GeoGebralla. Piirretään samaan koordinaatistoon käyrät ![]() ja
ja ![]() .
.

Yhtälön ratkaisuja ovat ![]() ja
ja ![]() .
.
Yhtälön algebralliset ratkaisut ovat:

tai

Ei ratkaisua, koska minkään luvun neliö ei voi olla negatiivinen.
Vastaus: Itseisarvoyhtälön ratkaisut ovat ![]() tai
tai ![]() .
.
Ratkaistaan itseisarvoyhtälö ![]() GeoGebralla. Piirretään samaan koordinaatistoon käyrät
GeoGebralla. Piirretään samaan koordinaatistoon käyrät ![]() ja
ja ![]() .
.

Yhtälön ratkaisuja ovat ![]() ja
ja ![]() .
.
Yhtälön algebralliset ratkaisut ovat:

Ratkaistaan toisen asteen yhtälö, jonka yleinen muoto on
![]()
Ratkaisukaava on
![]()
Ratkaistavassa yhtälössä ![]() vakioiden arvot ovat:
vakioiden arvot ovat:
![Rendered by QuickLaTeX.com \[\begin{cases}a&=1\\b&=-1\\c&=-2\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-2539ffcaaab3e184f62da2f136d4603f_l3.png)

tai
![]()
Ratkaistaan toisen asteen yhtälö, jossa
![Rendered by QuickLaTeX.com \[\begin{cases}a&=1\\b&=-1\\c&=2\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-0a6222819a9abdd3a3cc9e1f4f33f671_l3.png)

Ei ratkaisua, koska juurrettava on negaviivinen.
Vastaus: Itseisarvoyhtälön ratkaisut ovat ![]() tai
tai ![]() .
.
Ratkaistaan itseisarvoyhtälö ![]() GeoGebralla. Piirretään samaan koordinaatistoon käyrät
GeoGebralla. Piirretään samaan koordinaatistoon käyrät ![]() ja
ja ![]() .
.

Yhtälöllä ei näyttäisi olevan ratkaisuja.
Ratkaistaan itseisarvoyhtälö algebrallisesti.
![]()
Koska minkään luvun itseisarvo ei ole negatiivinen, yhtälöllä ei ole ratkaisua.
Piirretään GeoGebralla samaan koordinaatistoon käyrät ![]() ja
ja ![]() .
.

Yhtälön ratkaisuja ovat ![]() ja
ja ![]() .
.
Ratkaistaan yhtälö algebrallisesti.
![]()

tai

Vastaus: Yhtälön ratkaisut ovat ![]() ja
ja ![]() .
.
Piirretään GeoGebralla samaan koordinaatistoon käyrät ![]() ja
ja ![]() .
.

Yhtälön ratkaisuja ovat ![]() ,
, ![]() ,
, ![]() ja
ja ![]() .
.
Ratkaistaan yhtälö algebrallisesti.
![]() .
.
![]() tai
tai ![]()
![]()
Ratkaistaan toisen asteen yhtälö, jossa
![Rendered by QuickLaTeX.com \[\begin{cases}a&=1\\b&=-2\\c&=-3\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-38215269e443013806274364bb57270e_l3.png)

![]()
Ratkaistaan toisen asteen yhtälö, jossa
![Rendered by QuickLaTeX.com \[\begin{cases}a&=1\\b&=2\\c&=-3\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-6e8ba92796951bf6accd0b980c7cdf0d_l3.png)

Vastaus: Yhtälön ratkaisut ovat ![]() ,
, ![]() ,
, ![]() ja
ja ![]() .
.
Piirretään käyrä ![]() .
.
Kun ![]() , käyrän yhtälö on
, käyrän yhtälö on ![]() . Kun
. Kun ![]() , käyrän yhtälö on
, käyrän yhtälö on ![]() .
.
Siis
![Rendered by QuickLaTeX.com \[\begin{cases}y=-x,\ x<0\\y=x,\ x \geq 0\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-edd2c415fcfa02e07470d7171304609b_l3.png)

Käyrä voidaan myös piirtää siten, että piirretään käyrä ![]() ja peilataan
ja peilataan ![]() -akselin alapuoline osa
-akselin alapuoline osa ![]() -akselin yläpuolelle.
-akselin yläpuolelle.

Piirretään GeoGebralla käyrä ![]() samaan koordinaatistoon käyrän
samaan koordinaatistoon käyrän ![]() kanssa.
kanssa.

Yhtälön ![]() ratkaisu on
ratkaisu on ![]() tai
tai ![]() .
.
Piirretään GeoGebralla käyräparvi ![]() , jossa
, jossa ![]() on parametri.
on parametri.

Yllä olevassa kuvassa parametri ![]() saa arvoja välillä
saa arvoja välillä ![]() .
.
Sijoitetaan käyräparven yhtälössä ![]() pisteen
pisteen ![]() koordinaatit ja ratkaistaan parametri
koordinaatit ja ratkaistaan parametri ![]() .
.

Vastaus: Parametrin ![]() arvolla
arvolla ![]() käyrä kulkee pisteen
käyrä kulkee pisteen ![]() kautta.
kautta.
- 3.1 Suoran suunta: 301, 303a, 305, 309, 313.
- 3.2 Suoran yhtälö: 321, 326, 327a, 330, 331.
Suora ![]() , pisteet
, pisteet ![]() ja
ja ![]() .
.
Kulmakerroin ![]()
Suora ![]() , pisteet
, pisteet ![]() ja
ja ![]() .
.
Kulmakerroin ![]()
Suora ![]() , pisteet
, pisteet ![]() ja
ja ![]() .
.
Kulmakerroin ![]()
Pisteet ![]() ja
ja ![]() .
.
Kulmakerroin ![]()
Pisteet ![]() ja
ja ![]() .
.
Kulmakerroin ![]()
Pisteet ![]() ja
ja ![]() .
.
Kulmakerroin ![]()
Ei ole kulmakerrointa, koska suora on pystysuora.
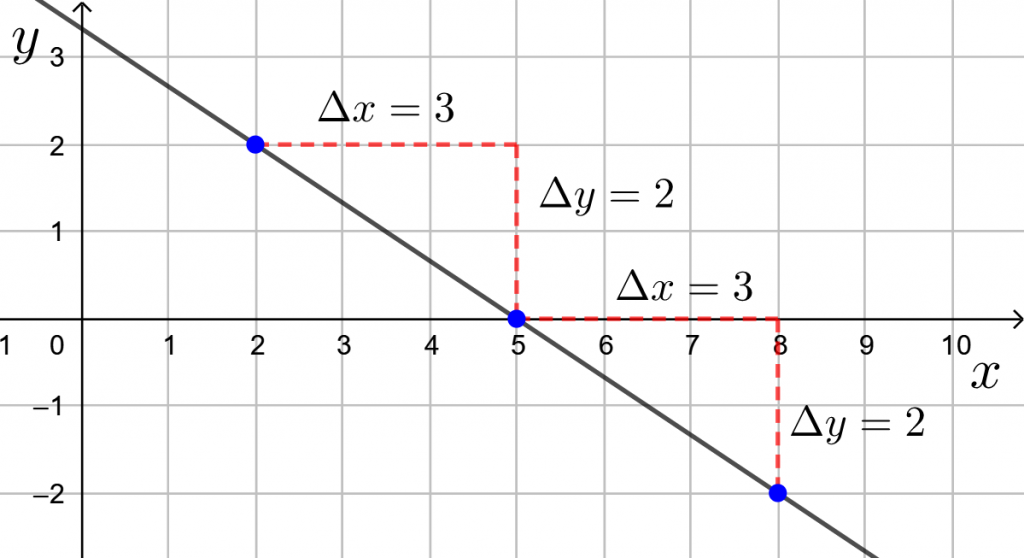
Suora kulkee pisteen ![]() kautta ja kulmakerroin on
kautta ja kulmakerroin on ![]() . Kun
. Kun ![]() -koordinaatti muuttuu oikealle yhden yksikön verran,
-koordinaatti muuttuu oikealle yhden yksikön verran, ![]() -koordinaatti muuttuu ylös kahden yksikön verran.
-koordinaatti muuttuu ylös kahden yksikön verran.
Siten toinen ![]() -koordinaatti on esimerkiksi
-koordinaatti on esimerkiksi ![]() ja
ja ![]() -koordinaatti on esimerkiksi
-koordinaatti on esimerkiksi ![]() eli koordinaatitksi tulee
eli koordinaatitksi tulee ![]() .
.
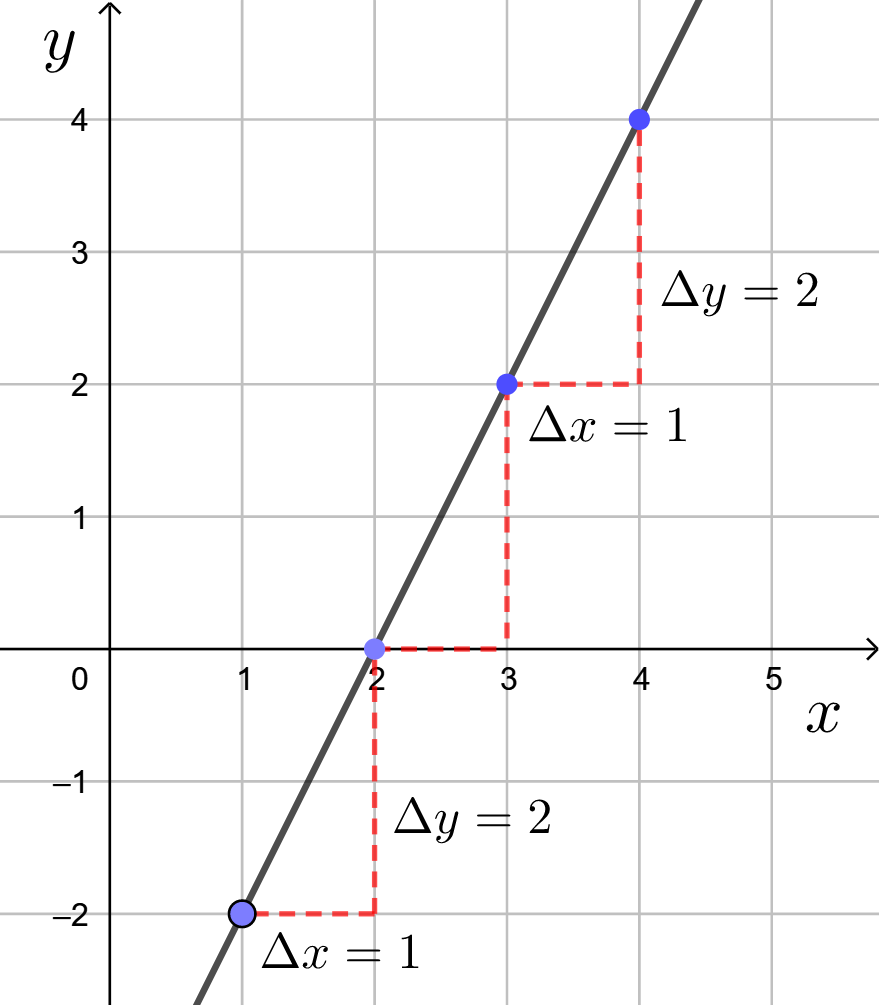
Suora kulkee pisteen ![]() kautta ja kulmakerroin on
kautta ja kulmakerroin on ![]() . Kun
. Kun ![]() -koordinaatti muuttuu oikealle neljän yksikön verran,
-koordinaatti muuttuu oikealle neljän yksikön verran, ![]() -koordinaatti muuttuu ylös kolmen yksikön verran.
-koordinaatti muuttuu ylös kolmen yksikön verran.
Siten toinen ![]() -koordinaatti on esimerkiksi
-koordinaatti on esimerkiksi ![]() ja
ja ![]() -koordinaatti on esimerkiksi
-koordinaatti on esimerkiksi ![]() eli koordinaatitksi tulee
eli koordinaatitksi tulee ![]() .
.
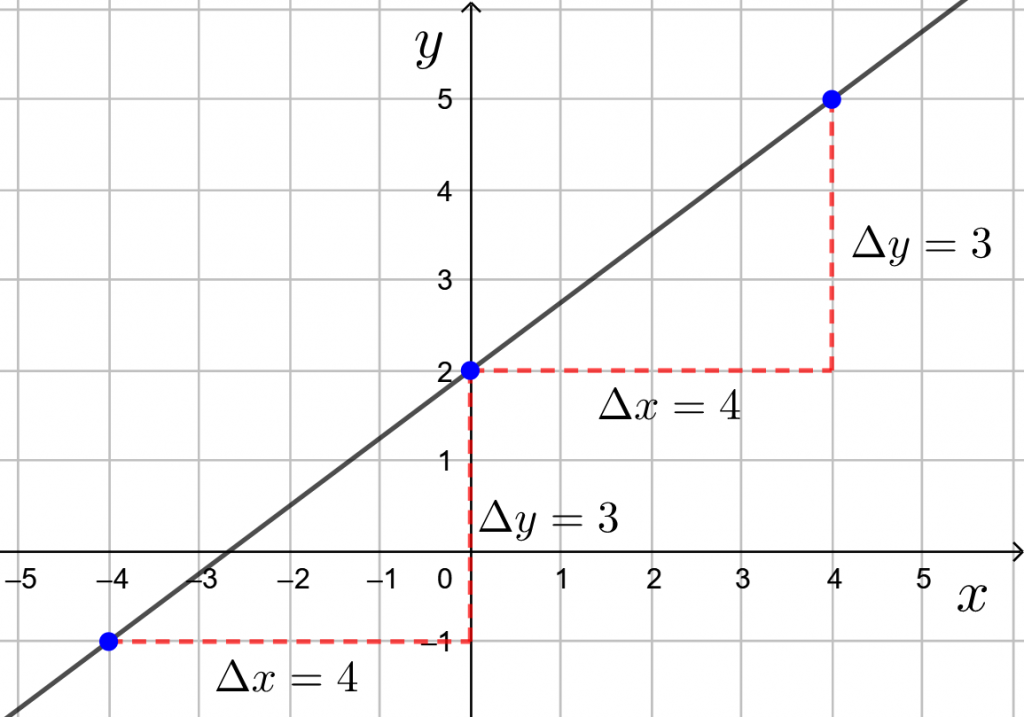
Suora kulkee pisteen ![]() kautta ja kulmakerroin on
kautta ja kulmakerroin on ![]() . Kun
. Kun ![]() -koordinaatti muuttuu oikealle kolmen yksikön verran,
-koordinaatti muuttuu oikealle kolmen yksikön verran, ![]() -koordinaatti muuttuu alas kahden yksikön verran.
-koordinaatti muuttuu alas kahden yksikön verran.
Siten toinen ![]() -koordinaatti on esimerkiksi
-koordinaatti on esimerkiksi ![]() ja
ja ![]() -koordinaatti on esimerkiksi
-koordinaatti on esimerkiksi ![]() eli koordinaatitksi tulee
eli koordinaatitksi tulee ![]() .
.