Tällä sivulla on
- Luvun 1.2 tuntimuistiinpanot torstaina 19.8.2021
- Tehtävien 116, 117, 119, 131, 132, 133, 136, 139, 141, 142 ja 147 ratkaisut.
Tehtävä 116. a)
Merkitään luvun ![]() etäisyys luvusta
etäisyys luvusta ![]() :
:![]()
Merkitään luvun ![]() etäisyys luvusta
etäisyys luvusta ![]() :
:![]()
Näiden etäisyyksin tulee olla yhtäsuuret. Nyt saadaan yhtälö
![]()
Yhtälö ![]() toteutuu täsmälleen silloin kun
toteutuu täsmälleen silloin kun ![]() tai
tai
![]() . Ratkaistaan molemmat yhtälöt.
. Ratkaistaan molemmat yhtälöt.
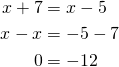
Ei ratkaisua.
Huom! Edellä olevan yhtälön ratkaisun voisi kirjoittaa myös seuraavasti:
![]()
Ei ratkaisua.
Ratkaistaan toinen yhtälö:
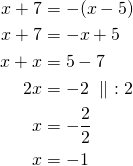
Tarkistetaan saatu ratkaisu. Sijoitetaan ![]() yhtälöön
yhtälöön ![]() :
:
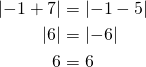
Vastaus: ![]()
Tehtävä 116. b)
Piirretään lukusuora ja merkitään luvut ![]() ja
ja ![]() lukusuoralle.
lukusuoralle.

Lukursuoralta huomataan, että luvun ![]() etäisyys luvuista
etäisyys luvuista ![]() ja
ja ![]() on yhtä suuri eli
on yhtä suuri eli ![]() . Siten luku
. Siten luku ![]() on yhtä etäällä kummastakin.
on yhtä etäällä kummastakin.
Tehtävä 117.
Lukujen ![]() ja
ja ![]() välinen etäisyys on
välinen etäisyys on
![]() .
.
Tämä etäisyys on yhtäsuuri kuin ![]() eli
eli ![]()
Yhtälö toteutuu täsmälleen silloin, kun ![]() tai
tai ![]() .
.
Ratkaistaan molemmat yhtälöt.
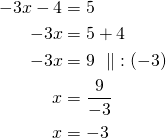
tai
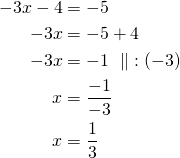
Sijoitetaan saadut ratkaisut ![]() ja
ja ![]() lausekkeisiin
lausekkeisiin ![]() ja
ja ![]() .
.
Kun ![]() , saadaan
, saadaan![]()
ja![]()
Siis kysytyt luvut ovat ![]() ja
ja ![]() .
.
Kun ![]() , saadaan
, saadaan
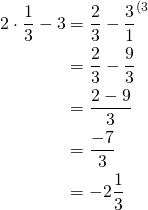
ja
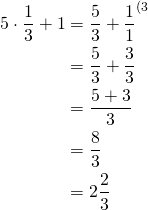
Siis kysytyt luvut ovat ![]() ja
ja ![]() .
.
Tehtävä 119. a)
Katso Appletti osoitteessa https://www.geogebra.org/m/hyNBY8MQ#material/sf8HWw2p
Tehtävä 119. b)
Lukujen ![]() ja
ja ![]() välinen etäisyys on
välinen etäisyys on ![]()
ja
lukujen ![]() ja
ja ![]() välinen etäisyys on
välinen etäisyys on ![]() .
.
Etäisyys luvusta ![]() on kolme kertaa niin suuri kuin etäisyys luvusta
on kolme kertaa niin suuri kuin etäisyys luvusta ![]() . Nyt saadaan yhtälö
. Nyt saadaan yhtälö ![]()
Sievennetään itseisarvon laskusääntöjen nojalla:
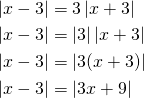
Yhtälö toteutuu täsmälleen silloin, kun ![]() tai
tai ![]() .
.
Ratkaistaan molemmat yhtälöt.
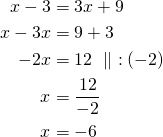
Toinen yhtälö
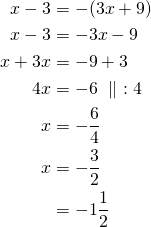
Vastaus: ![]() tai
tai ![]()
Tehtävä 131
A-III, B-II, C-IV, D-I
Tehtävä 132. a)
Epäyhtälö ![]() toteutuu täsmälleen silloin, kun luvun
toteutuu täsmälleen silloin, kun luvun ![]() etäisyys nollasta on pienempi kuin
etäisyys nollasta on pienempi kuin ![]() eli
eli ![]() .
.

Tehtävä 132. b)
Epäyhtälö ![]() toteutuu täsmälleen silloin, kun luvun
toteutuu täsmälleen silloin, kun luvun ![]() etäisyys
etäisyys
nollasta on pienempi kuin ![]() eli
eli ![]() .
.
Ratkaistaan kaksoisepäyhtälö:
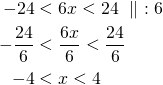
Epäyhtälön ratkaisu on ![]() .
.

Tehtävä 132. c)
Epäyhtälö ![]() toteutuu täsmälleen silloin, kun
toteutuu täsmälleen silloin, kun ![]() .
.
Ratkaistaan kaksoisepäyhtälö:
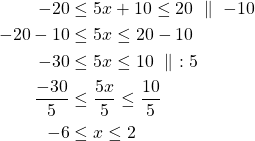

Tehtävä 132. d)
Epäyhtälö ![]() toteutuu täsmälleen silloin, kun
toteutuu täsmälleen silloin, kun ![]() .
.
Ratkaistaan kaksoisepäyhtälö:
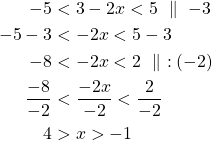
Epäyhtälön ratkaisu on ![]() .
.
Ratkaisun esitys lukusuoralla

Tehtävä 133. a)
Itseisarvoepäyhtälö ![]() tarkoittaa niitä lukuja
tarkoittaa niitä lukuja ![]() , joiden etäisyys nollasta on suurempi tai yhtäsuuri kuin 3.
, joiden etäisyys nollasta on suurempi tai yhtäsuuri kuin 3.
Epäyhtälö toteutuu, kun
![]() tai
tai ![]() .
.
Ratkaisun esitys lukusuoralla

Tehtävä 133. b)
Epäyhtälö ![]() toteutuu täsmälleen silloin, kun
toteutuu täsmälleen silloin, kun ![]() tai
tai ![]() .
.
Ratkaistaan molemmat epäyhtälöt.
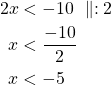
tai
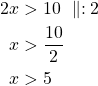
Epäyhtälön ratkaisu on ![]() tai
tai ![]() .
.
Ratkaisun esitys lukusuoralla

Tehtävä 133. c)
Epäyhtälö ![]() toteutuu täsmälleen silloin, kun
toteutuu täsmälleen silloin, kun ![]() tai
tai ![]() .
.
Ratkaistaan molemmat epäyhtälöt.
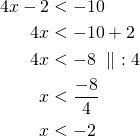
tai
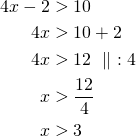
Epäyhtälön ratkaisu on ![]() tai
tai ![]() .
.
Ratkaisun esitys lukusuoralla

Tehtävä 133. d)
Epäyhtälö ![]() toteutuu täsmälleen silloin, kun
toteutuu täsmälleen silloin, kun ![]() tai
tai ![]() .
.
Ratkaistaan molemmat epäyhtälöt.
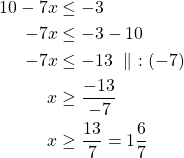
tai
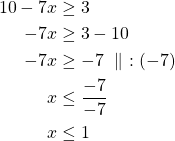
Epäyhtälön ratkaisu on ![]() tai
tai ![]() .
.
Ratkaisun esitys lukusuoralla

Tehtävä 134 a)
Epäyhtälö ![]() tarkoittaa niitä kokonaislukuja
tarkoittaa niitä kokonaislukuja ![]() , joiden etäisyys nollasta on suurempi kuin
, joiden etäisyys nollasta on suurempi kuin ![]() .
.
Tehtävässä annetuista kokonaisluvuista ![]() vain luvut
vain luvut ![]() ja
ja ![]() toteuttavat epäyhtälön.
toteuttavat epäyhtälön.
Tehtävä 134 b)
Epäyhtälö ![]() tarkoittaa niitä kokonaislukuja
tarkoittaa niitä kokonaislukuja ![]() , joiden etäisyys nollasta on pienempi tai yhtä suuri kuin
, joiden etäisyys nollasta on pienempi tai yhtä suuri kuin ![]() .
.
Kokonaisluvuista ![]() luvut
luvut ![]() ja
ja ![]() toteuttavat epäyhtälön.
toteuttavat epäyhtälön.
Tehtävä 134 c)
Epäyhtälö ![]() tarkoittaa niitä lukuja
tarkoittaa niitä lukuja ![]() , joiden etäisyys nollasta on
, joiden etäisyys nollasta on
pienempi kuin ![]() .
.
Kokonaisluvuista ![]() luvut
luvut ![]() ja
ja ![]() toteuttavat epäyhtälön.
toteuttavat epäyhtälön.
Tehtävä 134 d)
Epäyhtälö ![]() tarkoittaa niitä lukuja
tarkoittaa niitä lukuja ![]() , joiden etäisyys nollasta on
, joiden etäisyys nollasta on
suurempi tai yhtä suuri kuin ![]() .
.
Kokonaisluvuista ![]() luvut
luvut ![]() ja
ja ![]() toteuttavat epäyhtälön.
toteuttavat epäyhtälön.
Tehtävä 135 a)
Epäyhtälö ![]() on aina epätosi, koska minkään luvun itseisarvo ei ole negatiivinen. Siten itseisarvo ei voi olla pienempi kuin negatiivinen luku.
on aina epätosi, koska minkään luvun itseisarvo ei ole negatiivinen. Siten itseisarvo ei voi olla pienempi kuin negatiivinen luku.
Tehtävä 135 b)
Epäyhtälö ![]() aina tosi, koska itseisarvo on aina suurempi tai yhtä suuri kuin nolla.
aina tosi, koska itseisarvo on aina suurempi tai yhtä suuri kuin nolla.
Tehtävä 135 c)
Epäyhtälö ![]() on aina tosi, koska itseisarvo
on aina tosi, koska itseisarvo ![]() ja luvun neliö
ja luvun neliö ![]() , siis myös näiden summa
, siis myös näiden summa ![]() .
.
Tehtävä 135 d)
Vain luku![]() , jolloin lauseke
, jolloin lauseke ![]() , toteuttaa epäyhtälön
, toteuttaa epäyhtälön ![]() , koska itseisarvo on aina suurempi tai yhtä suuri kuin nolla.
, koska itseisarvo on aina suurempi tai yhtä suuri kuin nolla.
Tehtävä 136. a)
Itseisarvoepäyhtälö ![]() toteutuu täsmälleen silloin, kun
toteutuu täsmälleen silloin, kun![]() .
.
Ratkaistaan kaksoisepäyhtälö:
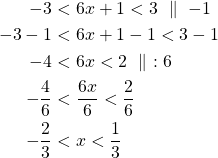
Vastaus: Epäyhtälön ratkaisu on ![]() .
.
Tehtävä 136. b)
Itseisarvoepäyhtälö ![]() toteutuu täsmälleen silloin, kun
toteutuu täsmälleen silloin, kun![]() tai
tai ![]() .
.
Ratkaistaan molemmat epäyhtälöt.
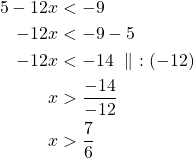
tai
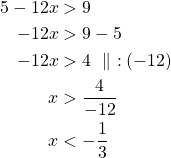
Vastaus: Epäyhtälön ratkaisu on ![]() tai
tai ![]() .
.
Tehtävä 136. c)
Itseisarvoepäyhtälö ![]() toteutuu täsmälleen silloin, kun
toteutuu täsmälleen silloin, kun![]() .
.
Ratkaistaan kaksoisepäyhtälö:
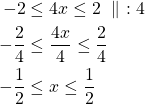
Vastaus: Epäyhtälön ratkaisu on ![]() .
.
Tehtävä 136. d)
Itseisarvoepäyhtälö ![]() toteutuu täsmälleen silloin, kun
toteutuu täsmälleen silloin, kun![]() tai
tai ![]() .
.
Ratkaistaan molemmat epäyhtälöt.
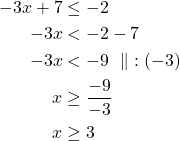
tai
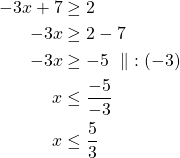
Vastaus: Epäyhtälön ratkaisu on ![]() tai
tai ![]() .
.
Tehtävä 139. a)
Luvun ![]() etäisyys luvusta
etäisyys luvusta ![]() on
on ![]() . Tämän etäisyyden tulee olla enintään (eli korkeintaan)
. Tämän etäisyyden tulee olla enintään (eli korkeintaan) ![]() .
.
Saadaan epäyhtälö ![]() .
.
Ratkaistaan kaksoisepäyhtälö:
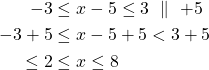
Välillä ![]() olevat luvut toteuttavat ehdon.
olevat luvut toteuttavat ehdon.
Tehtävä 139. b)
Luvun ![]() etäisyys luvusta
etäisyys luvusta ![]() on
on ![]() . Tämän etäisyyden tulee olla suurempi kuin (eli enemmän kuin) 7.
. Tämän etäisyyden tulee olla suurempi kuin (eli enemmän kuin) 7.
Saadaan epäyhtälö ![]() . Epäyhtälö toteutuu täsmälleen silloin, kun
. Epäyhtälö toteutuu täsmälleen silloin, kun ![]() tai
tai ![]() .
.
Ratkaistaan molemmat epäyhtälöt.
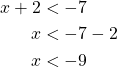
tai
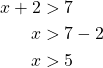
Väleillä ![]() tai
tai ![]() olevat luvut toteuttavat ehdon.
olevat luvut toteuttavat ehdon.
Tehtävä 141 a)
Tässä tehtävässä tarvitaan neliöönkorotuslausetta.
Ei-negatiivisille luville ![]() ja
ja ![]() pätee
pätee
![]() jos ja vain jos
jos ja vain jos ![]()
Koska itseisarvot ovat ei-negatiivisia, voidaan neliöönkorotuslauseen perusteella korottaa epäyhtälön
![]()
Tällöin epäyhtälön
![]()
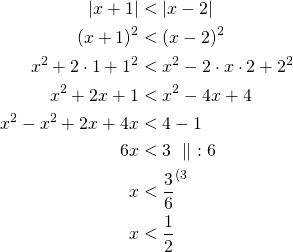
Vastaus: Epäyhtälön ratkaisu on ![]() .
.
Tehtävä 141 b)
Koska itseisarvot ovat ei-negatiivisia, voidaan epäyhtälön
![]()
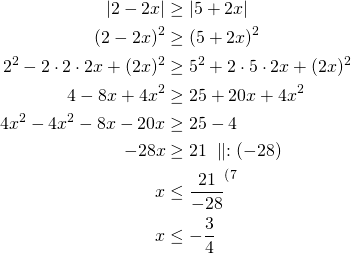
Vastaus: Epäyhtälön ratkaisu on ![]() .
.
Tehtävä 142. a)
Koska itseisarvot ovat ei-negatiivisia, voidaan epäåyhtälön ![]() molemmat puolet korottaa neliöön eli toiseen potenssiin.
molemmat puolet korottaa neliöön eli toiseen potenssiin.
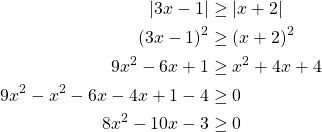
Ratkaistaan toisen asteen funktion ![]() nollakohdat yhtälöstä
nollakohdat yhtälöstä ![]()
Toisen asteen yhhälön ratkaisukaavalla saadaan

Funktion ![]() toisen asteen kerroin 8 on positiivinen, joten funktion kuvaaja on ylöspäin aukeava paraabeli.
toisen asteen kerroin 8 on positiivinen, joten funktion kuvaaja on ylöspäin aukeava paraabeli.
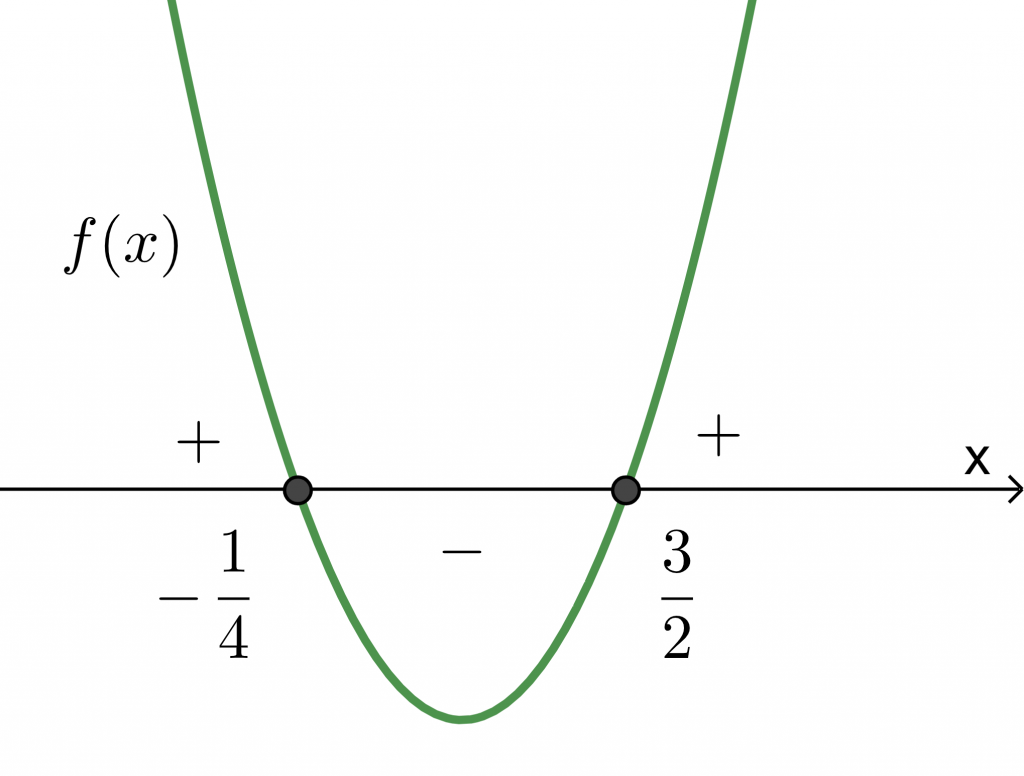
Epäyhtälön ![]() ja samalla epäyhtälön
ja samalla epäyhtälön ![]() ratkaisu on
ratkaisu on
![]() tai
tai ![]() .
.
Tehtävä 142. b)
Koska itseisarvot ovat ei-negatiivisia, voidaan epäåyhtälön ![]() molemmat puolet korottaa neliöön eli toiseen potenssiin.
molemmat puolet korottaa neliöön eli toiseen potenssiin.
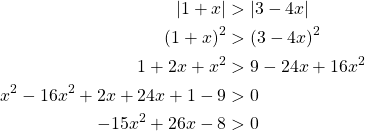
Ratkaistaan toisen asteen funktion ![]() nollakohdat yhtälöstä
nollakohdat yhtälöstä ![]()
Toisen asteen yhhälön ratkaisukaavalla saadaan

Funktion ![]() toisen asteen kerroin
toisen asteen kerroin ![]() on negatiivinen, joten funktion kuvaaja on alaspäin aukeava paraabeli.
on negatiivinen, joten funktion kuvaaja on alaspäin aukeava paraabeli.
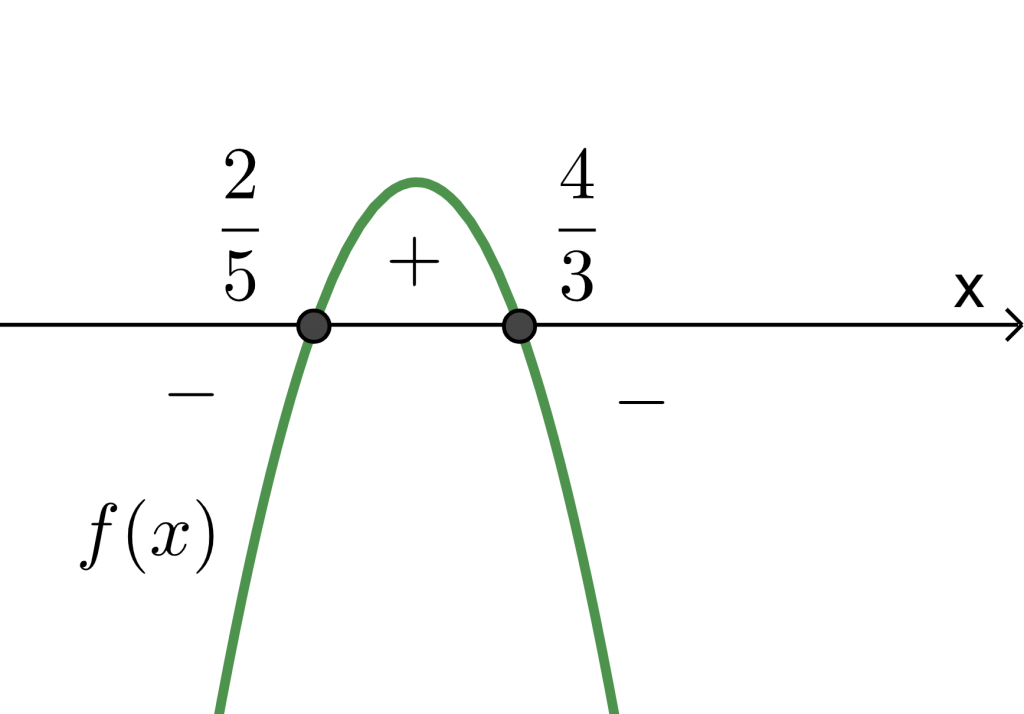
Epäyhtälön ![]() ja samalla epäyhtälön
ja samalla epäyhtälön ![]() ratkaisu on
ratkaisu on
![]() .
.
Tehtävä 147 a)
Neliöjuuri on määritelty, kun juurrettava on ei-negatiivinen. Luvun
neliö ![]() on aina ei-negatiivinen, joten
on aina ei-negatiivinen, joten ![]() . Tällöin lauseke
. Tällöin lauseke
![]()
on määritelty kaikilla muuttujan ![]() arvoilla.
arvoilla.
Tehtävä 147 b)
Yhtälön molemmat puolet ovat ei-negatiivisia, joten voidaan käyttää neliöönkorotuslausetta.
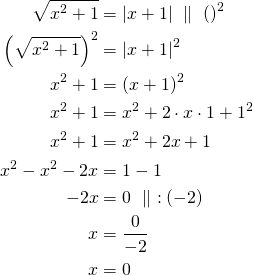
Vastaus: Yhtälön ratkaisu on ![]() .
.