Tällä sivulla on
- Tuntimuistiipanot luvusta 1.1. tiistaina 17.8.2021 ja torstaina 19.8.2021
- Luku 1.1: Tehtävät 102 – 110, 112c, 113c, 114a, 114c, 126
Tehtävä 102
a) ![]() .
.
b) Luvun etäisyys nollasta lukusuoralla on luvun itseisarvo. Siten![]() .
.
c) Etäisyydellä ![]() nollasta ovat luvut, joiden itseisarvo on
nollasta ovat luvut, joiden itseisarvo on ![]() . Luvut ovat
. Luvut ovat ![]() ja
ja ![]() .
.
d) Luvun ![]() itseisarvo on
itseisarvo on ![]() . Luvun
. Luvun ![]() itseisarvo on
itseisarvo on ![]() .
.
Luvut ovat ![]() ja
ja ![]() .
.
Tehtävä 103
a) Koska ![]() ja
ja ![]() , luku
, luku ![]() on suurempi.
on suurempi.
b) Koska a-kohdassa pääteltiin, että ![]() on pienempi kuin
on pienempi kuin ![]() eli
eli ![]() , niin lauseke
, niin lauseke ![]() .
.
Jos luku on negatiivinen eli pienempi kuin nolla, niin sen itseisarvo on luvun vastaluku.
![]() .
.
Tehtävä 104
Selvitetään kaikissa kohdissa, onko itseisarvomerkkien sisällä oleva luku positiivinen vai negatiivinen.
a) ![]() . Siten luku
. Siten luku ![]() on pienempi kuin nolla eli negatiivinen.
on pienempi kuin nolla eli negatiivinen.
Negatiivisen luvun itseisarvo on luvun vastaluku.![]()
b) Koska luku ![]() , niin
, niin ![]() . Siten
. Siten ![]() .
.
Negatiivisen luvun itseisarvo on luvun vastaluku.![]() .
.
c) Koska luku ![]() ja toisaalta
ja toisaalta ![]() , on luku
, on luku ![]() .
.
Positiivisen luvun itseisarvo on luku itse.![]() .
.
Tehtävä 105
a) Luvun ![]() itseisarvo on 1, eli luvun etäisyys nollasta on 1. Lukujen -1 ja 1 etäisyys nollasta on 1, koska
itseisarvo on 1, eli luvun etäisyys nollasta on 1. Lukujen -1 ja 1 etäisyys nollasta on 1, koska ![]() ja
ja ![]() .
.
Alla oleva kuva on tehty GeoGebralla.

b) Luvun ![]() itseisarvo on 3, eli luvun etäisyys nollasta on 3. Lukujen -3 ja 3 etäisyys nollasta on 3, koska
itseisarvo on 3, eli luvun etäisyys nollasta on 3. Lukujen -3 ja 3 etäisyys nollasta on 3, koska ![]() ja
ja ![]() .
.

c) Yhtälöllä ![]() ei ole ratkaisua, koska minkään luvun itseisarvo ei ole negatiivinen luku.
ei ole ratkaisua, koska minkään luvun itseisarvo ei ole negatiivinen luku.
Tehtävä 106
a) Yhtälö ![]() toteutuu, kun luvun
toteutuu, kun luvun ![]() etäisyys nollasta on 4. Lukujen -4 ja 4 etäisyys nollasta on 4.
etäisyys nollasta on 4. Lukujen -4 ja 4 etäisyys nollasta on 4.
Saadaan yhtälöt
![]() tai
tai ![]() .
.
Ratkaistaan molemmat yhtälöt.

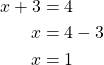
Tarkistus:
Kun ![]() :
: ![]()
Kun ![]() :
: ![]()
Vastaus: Yhtälöt ratkaisut ovat ![]() ja
ja ![]() .
.
b) Yhtälö ![]() toteutuu, kun luvun
toteutuu, kun luvun ![]() etäisyys nollasta on 7. Lukujen -7 ja 7 etäisyys nollasta on 7.
etäisyys nollasta on 7. Lukujen -7 ja 7 etäisyys nollasta on 7.
Saadaan yhtälöt
![]() tai
tai ![]() .
.
Ratkaistaan molemmat yhtälöt.

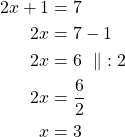
Tarkistus:
Kun ![]() :
: ![]()
Kun ![]() :
: ![]()
Vastaus: Yhtälöt ratkaisut ovat ![]() ja
ja ![]() .
.
c) Luvun ![]() etäisyys nollasta pitää olla nolla. Yhtälöllä on vain yksi ratkaisu
etäisyys nollasta pitää olla nolla. Yhtälöllä on vain yksi ratkaisu ![]() .
.
Tehtävä 107
Tässä tehtävässä käytetään kirjan sivulla 13 olevaa lausetta:
![]()
a) Yhtälö ![]() toteutuu täsmälleen silloin, kun
toteutuu täsmälleen silloin, kun![]() tai
tai ![]() .
.
Ratkaistaan molemmat yhtälöt.
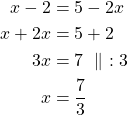
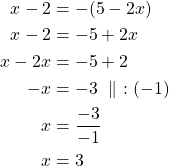
Tarkistus GeoGebralla.
- Kirjoita GeGebrassa CAS-näkymässä
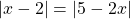 .
. - Paina enteriä.
- Klikkaa painetta x =
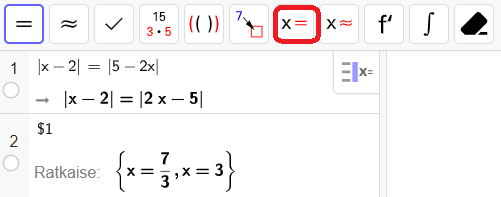
Toinen tapa on kirjoittaa suoraan komento Ratkaise(), jonka sulkeiden sisään kirjoitetaan ratkaistava yhtälö ![]() ja pilkun jälkeen, minkä muuttujan suhteen yhtälö ratkaistaan.
ja pilkun jälkeen, minkä muuttujan suhteen yhtälö ratkaistaan.
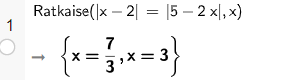
Koska ratkaistavssa yhtälössä on muuttujana vain ![]() , myös komento
, myös komento
Ratkaise( ![]() ) toimisi oikein.
) toimisi oikein.
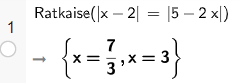
Vastaus: Yhtälön ratkaisut ovat ![]() tai
tai ![]() .
.
b) Yhtälö ![]() toteutuu täsmälleen silloin, kun
toteutuu täsmälleen silloin, kun![]() tai
tai ![]() .
.
Ratkaistaan molemmat yhtälöt.
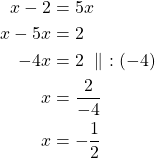
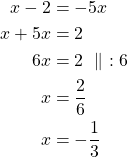
Vastaus: Yhtälön ratkaisut ovat ![]() tai
tai ![]() .
.
c) Siirretään ensin yhtälön ![]() itseisarvolausekkeet eri puolille yhtäsuuruusmerkkiä.
itseisarvolausekkeet eri puolille yhtäsuuruusmerkkiä.
![]()
Yhtälö ![]() toteutuu täsmälleen silloin, kun
toteutuu täsmälleen silloin, kun![]() tai
tai ![]() .
.
Ratkaistaan molemmat yhtälöt.
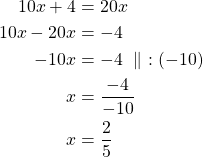
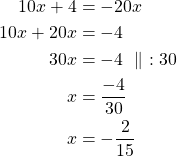
Vastaus: Yhtälön ratkaisut ovat ![]() tai
tai ![]() .
.
Tehtävä 108
a) ![]()
b) ![]()
c) ![]()
Tehtävä 109
a) Tutkitaan ensin, kumpi luvuista, 3 vai ![]() on pienempi (tai suurempi).
on pienempi (tai suurempi).
Koska ![]() , niin
, niin ![]() . Tällöin
. Tällöin ![]() .
.
Koska luku ![]() on pienempi kuin nolla eli se on negatiivinen, niin sen itseisarvo on luvun vastaluku.
on pienempi kuin nolla eli se on negatiivinen, niin sen itseisarvo on luvun vastaluku.
![]()
b) Tutkitaan ensin, kumpi luvuista, ![]() vai
vai ![]() on pienempi (tai suurempi).
on pienempi (tai suurempi).
Koska ![]() ja
ja ![]() ,
,
niin ![]() . Tällöin
. Tällöin ![]() .
.
Koska luku ![]() on suurempi kuin nolla eli se on positiivinen, niin sen itseisarvo on luku itse.
on suurempi kuin nolla eli se on positiivinen, niin sen itseisarvo on luku itse.
![]() .
.
c) Koska ![]() on negatiivinen luku, sen itseisarvo on luvun vastaluku.
on negatiivinen luku, sen itseisarvo on luvun vastaluku.
![]() .
.
Tehtävä 110
a) Aloitetaan siirtämällä termi ![]() yhtäsuuruusmerkin oikealle puolelle.
yhtäsuuruusmerkin oikealle puolelle.
![]()
Luvut, joiden etäisyys nollasta on 5, ovat -5 ja 5.
Saadaan kaksi yhtälöä:
![]() ja
ja ![]()
Ratkaistaan molemmat yhtälöt.
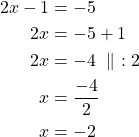
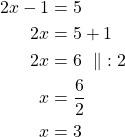
Vastaus: Yhtälön ratkaisut ovat ![]() ja
ja ![]() .
.
b) Vain luvun nolla itseisarvo on nolla.
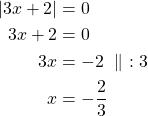
Vastaus: Yhtälön ratkaisu on ![]() .
.
c) Yhtälöllä ei ole ratkaisua, koska minkään luvun itseisarvo ei ole negatiivinen.
Tehtävä 112b
Yhtälö![]() toteutuu, kun
toteutuu, kun![]() tai
tai ![]() .
.
Ratkaistaan molemmat yhtälöt.
Ratkaistaan ensin yhtälö ![]()
![]()
Vastaus: Yhtälön ratkaisut ovat ![]() ja
ja ![]() .
.
Ratkaistaan 2. asteen yhtälön ratkaisukaavalla, jossa
![Rendered by QuickLaTeX.com \[\begin{cases}a&=1\\b&=-1\\c&=-2\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-c8e46a335a1f0a600205bc71e551a72a_l3.png)

Ratkaistaan toinen yhtälö ![]()

Ei ratkaisua, koska neliöjuuren sisällä oleva luku on negatiivinen.
Vastaus: Yhtälön ratkaisut ovat ![]() tai
tai ![]() .
.
Tehtävä 112c
Yhtälö ![]() toteutuu, kun
toteutuu, kun
![]() tai
tai ![]() .
.
Ratkaistaan ensin yhtälö ![]() .
.
![Rendered by QuickLaTeX.com \begin{align*} x^3+ \frac{7}{16}&=\frac{9}{16} \\ x^3&=\frac{9}{16} - \frac{7}{16}\\ x^3&=\frac{9-7}{16} \\ x^3&=\frac{2}{16} \\ x^3&=\frac{1}{8}\ \parallel\ \sqrt[3]{\ }\\ x^3&=\sqrt[3]{\frac{1}{8}} \\ x&=\frac{1}{2}\end{align*}](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-5d9892aa14f4be33e1e8975b7e2f7b79_l3.png)
Ratkaistaan sitten yhtälö ![]() .
.
![Rendered by QuickLaTeX.com \begin{align*} x^3+ \frac{7}{16}&=-\frac{9}{16} \\ x^3&=-\frac{9}{16} - \frac{7}{16}\\ x^3&=\frac{-9-7}{16} \\ x^3&=\frac{-16}{16} \\ x^3&=-\frac{16}{16} \\ x^3&=-1\ \parallel\ \sqrt[3]{\ }\\ x&=-1\end{align*}](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-fe3c82b75bdcd3383fdb29c8f05611bd_l3.png)
Vastaus: Yhtälön ratkaisut ovat ![]() tai
tai ![]() .
.
Tehtävä 113c
![]() .
.
Tämän ratkaisu perustuu seuraavaan itseisarvon ominaisuuteen, joka on lauseen kirjan sivulla 13.
![]() jos ja vain jos
jos ja vain jos ![]() tai
tai ![]() .
.
Kirjoitetaan ensimmäinen yhtälö, jossa
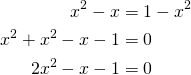
Ratkaistaan 2. asteen yhtälön ratkaisukaavalla, jossa
![Rendered by QuickLaTeX.com \[\begin{cases}a&=2\\b&=-1\\c&=-1\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-630a235f1d21446fdd9a96446d4cc8d7_l3.png)
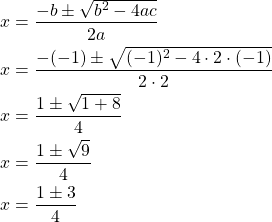
Tämän ratkaisut ovat
![]()
tai
![]()
Kirjoitetaan toinen yhtälö, jossa
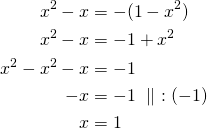
Ratkaisuiksi saatiin ![]() sekä kahdesti
sekä kahdesti ![]() (joita ei kirjoiteta kahteen kertaan).
(joita ei kirjoiteta kahteen kertaan).
Vastaus: Yhtälön ratkaisut ovat ![]() ja
ja ![]() .
.
Tehtävä 114a
Yhtälö![]() toteutuu, kun
toteutuu, kun
![]() tai
tai ![]() .
.
Ratkaistaan ensin yhtälö ![]() .
.
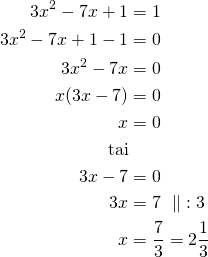
Ratkaistaan sitten yhtälö ![]() .
.

Ratkaistaan 2. asteen yhtälön ratkaisukaavalla, jossa
![Rendered by QuickLaTeX.com \[\begin{cases}a&=3\\b&=-7\\c&=2\end{cases}\]](https://blogit.gradia.fi/ageom/wp-content/ql-cache/quicklatex.com-65924f3ef5f9c151a9488d717a4895aa_l3.png)
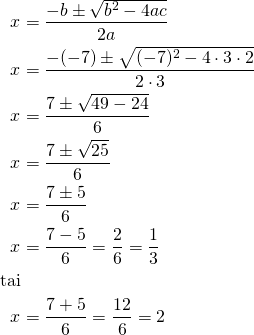
Ilmoitetaan ratkaisussa saadut ![]() :n arvot suuruusjärjestyksessä.
:n arvot suuruusjärjestyksessä.
Vastaus: Yhtälön ratkaisut ovat ![]() ,
, ![]() ,
, ![]() tai
tai ![]() .
.
Tehtävä 114c
Ratkaise yhtälö ![]() .
.
Kahden itseisarvon summa voi olla nolla vain silloin, kun molemmat itseisarvot ovat nollia. Siten merkitään
![]() ja
ja ![]() .
.
Ratkaistaan ensin yhtälö ![]() .
.
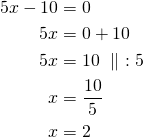
Ratkaistaan sitten yhtälö ![]() .
.
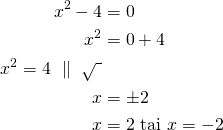
Saatiin ratkaisuiksi ![]() ja
ja ![]() tai
tai ![]() . Molemmat yhtälöt toteutuvat, kun
. Molemmat yhtälöt toteutuvat, kun ![]() .
.
Vastus: Yhtälön ratkaisu on ![]() .
.
Tehtävä 126
Koska minkään luvun itseisarvo ei ole negatiivinen, tutkitaan, milloin itseisarvon määritelmän perusteella yhtälöllä![]() on ratkaisuja.
on ratkaisuja.
Ratkaisuja on vain, kun ![]() .
.
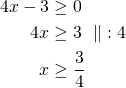
Vain sellaiset vastaukset kelpaavat, jotka toteuttavat ehdon ![]() .
.
Ratkaisu ei ole oikein, jos hyväksytään kaikki vastausvaihtoehdot. Jätetään vastauksesta pois ![]() .
.
Vastaus: ![]() .
.